Diamonds - Preprocessing
1. Analyse du dataset pour l'encodage
2. Encodage (ordinal)
3. Analyse du dataset pour la normalisation
4. Normalization MinMax
5. Standartisation
2. Encodage (ordinal)
3. Analyse du dataset pour la normalisation
4. Normalization MinMax
5. Standartisation
1. Analyse du dataset pour l'encodage
Analyse du Dataset
df = sns.load_dataset('diamonds')
df.head()
carat cut color clarity depth table price x y z 0 0.23 Ideal E SI2 61.5 55.0 326 3.95 3.98 2.43 1 0.21 Premium E SI1 59.8 61.0 326 3.89 3.84 2.31 2 0.23 Good E VS1 56.9 65.0 327 4.05 4.07 2.31 3 0.29 Premium I VS2 62.4 58.0 334 4.20 4.23 2.63 4 0.31 Good J SI2 63.3 58.0 335 4.34 4.35 2.75
3 colonnes ne sont pas numériques et ont une hiérachie :
- 'cut' : Qualité de la découpe du diamand
- 'color' : Qualité de la couleur du diamand
- 'clarity' : Qualité de la transparence du diamand
- 'cut' : Qualité de la découpe du diamand
- 'color' : Qualité de la couleur du diamand
- 'clarity' : Qualité de la transparence du diamand
Liste des valeurs de la colonne 'cut'
df['cut'].unique()
['Ideal', 'Premium', 'Good', 'Very Good', 'Fair'] Categories (5, object): ['Ideal', 'Premium', 'Very Good', 'Good', 'Fair']
Liste des valeurs de la colonne 'color'
df['color'].unique()
['E', 'I', 'J', 'H', 'F', 'G', 'D'] Categories (7, object): ['D', 'E', 'F', 'G', 'H', 'I', 'J']
Liste des valeurs de la colonne 'clarity'
df['clarity'].unique()
['SI2', 'SI1', 'VS1', 'VS2', 'VVS2', 'VVS1', 'I1', 'IF'] Categories (8, object): ['IF', 'VVS1', 'VVS2', 'VS1', 'VS2', 'SI1', 'SI2', 'I1']
2. Encodage (ordinal)
Ordinal Encoder
cut_order = ['Very Bad', 'Bad', 'Fair', 'Good', 'Very Good', 'Premium', 'Ideal']
color_order = ['J', 'I', 'H', 'G', 'F', 'E', 'D']
clarity_order = ['I1', 'SI2', 'SI1', 'VS2', 'VS1', 'VVS2', 'VVS1', 'IF']
encoder = OrdinalEncoder(
categories=[cut_order, color_order, clarity_order],
handle_unknown='use_encoded_value',
unknown_value=-1
)
encoder.fit(df[['cut', 'color', 'clarity']])
encoder.transform(df[['cut', 'color', 'clarity']])
[[4. 5. 1.] [3. 5. 2.] [1. 5. 4.] ... [2. 6. 2.] [3. 2. 1.] [4. 6. 1.]]
Si de nouvelles données...
encoder.transform([['Fair', 'G', 'A+']])
[[ 0. 3. -1.]]
Remarque
Il est intéressant d'ajouter des catégories qui n'existent pas encore dans le dataset (Par exemple 'Bad', 'Very Bad')
Il est intéressant d'ajouter des catégories qui n'existent pas encore dans le dataset (Par exemple 'Bad', 'Very Bad')
3. Analyse du dataset pour la normalisation
df_numeric = df.select_dtypes(exclude='category')
df_numeric.describe(include='all', exclude = None)
carat depth ... y z count 53940.000000 53940.000000 ... 53940.000000 53940.000000 mean 0.797940 61.749405 ... 5.734526 3.538734 std 0.474011 1.432621 ... 1.142135 0.705699 min 0.200000 43.000000 ... 0.000000 0.000000 25% 0.400000 61.000000 ... 4.720000 2.910000 50% 0.700000 61.800000 ... 5.710000 3.530000 75% 1.040000 62.500000 ... 6.540000 4.040000 max 5.010000 79.000000 ... 58.900000 31.800000 [8 rows x 7 columns]
Les variables numériques sont 'carat', 'depth', 'table', 'price', 'x', 'y', 'z'
Variable 'carat'
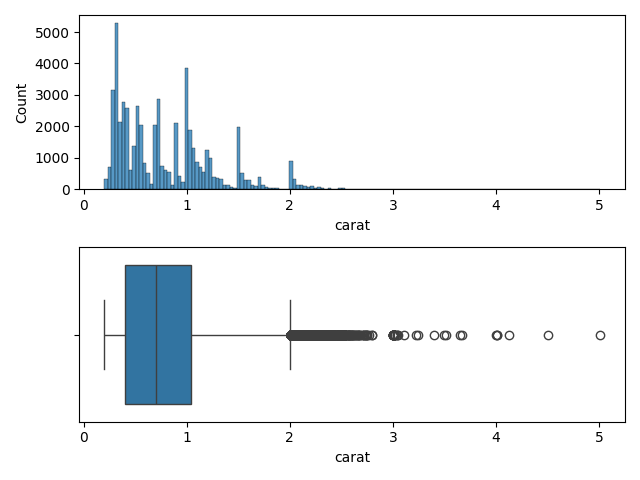
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='carat', ax=ax[0])
sns.boxplot(data=df_numeric, x='carat', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'carat'
Beaucoup de outliers et pas d'allure Gaussienne
Il faudra décomposer la variable 'carat' en plusieurs sous-variables...
Beaucoup de outliers et pas d'allure Gaussienne
Il faudra décomposer la variable 'carat' en plusieurs sous-variables...
Variable 'depth'
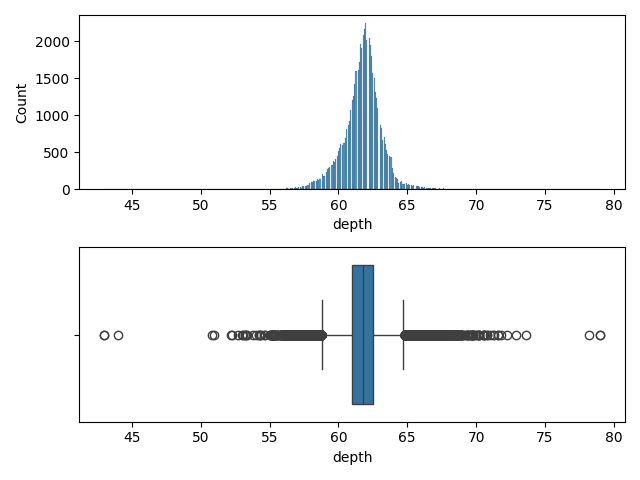
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='depth', ax=ax[0])
sns.boxplot(data=df_numeric, x='depth', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'depth'
Beaucoup de outliers mais une allure Gaussienne
=> Normalisation par Standardisation
Beaucoup de outliers mais une allure Gaussienne
=> Normalisation par Standardisation
Variable 'table'
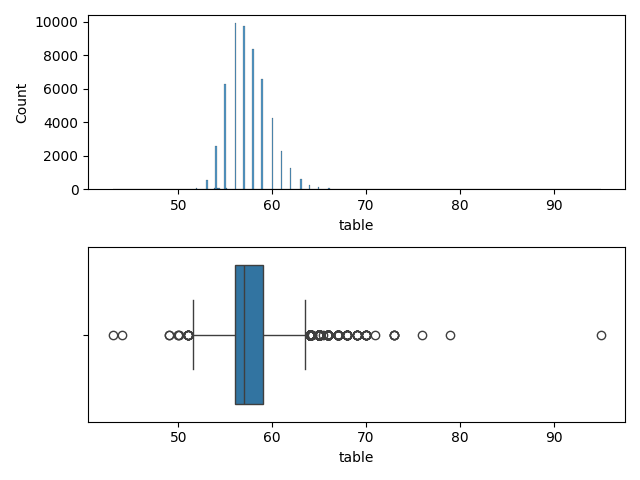
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='table', ax=ax[0])
sns.boxplot(data=df_numeric, x='table', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'table'
Beaucoup de outliers mais une allure Gaussienne
=> Normalisation par Standardisation
Beaucoup de outliers mais une allure Gaussienne
=> Normalisation par Standardisation
Variable 'price'
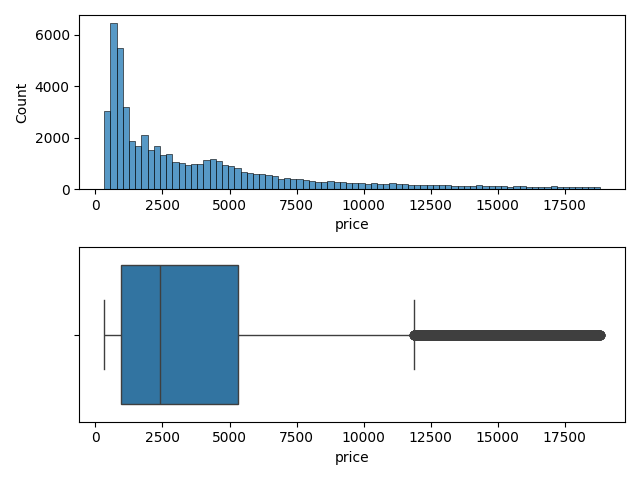
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='price', ax=ax[0])
sns.boxplot(data=df_numeric, x='price', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'price'
Beaucoup de outliers et pas d'allure Gaussienne
=> Normalisation MinMax
Beaucoup de outliers et pas d'allure Gaussienne
=> Normalisation MinMax
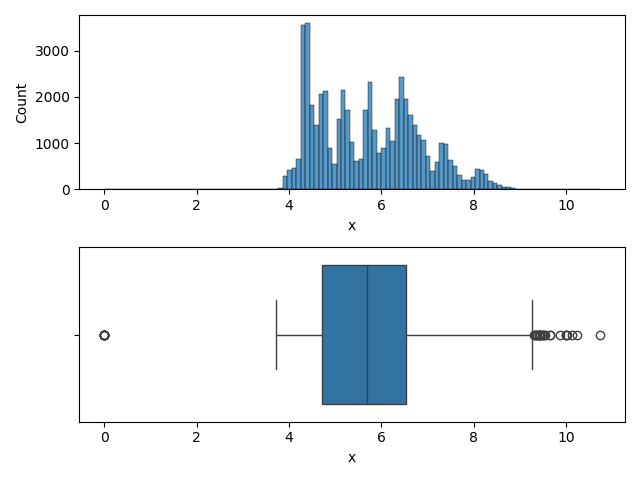
Variable 'x'
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='x', ax=ax[0])
sns.boxplot(data=df_numeric, x='x', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'x'
Des outliers et une allure Gaussienne => Standardisation
Des outliers et une allure Gaussienne => Standardisation
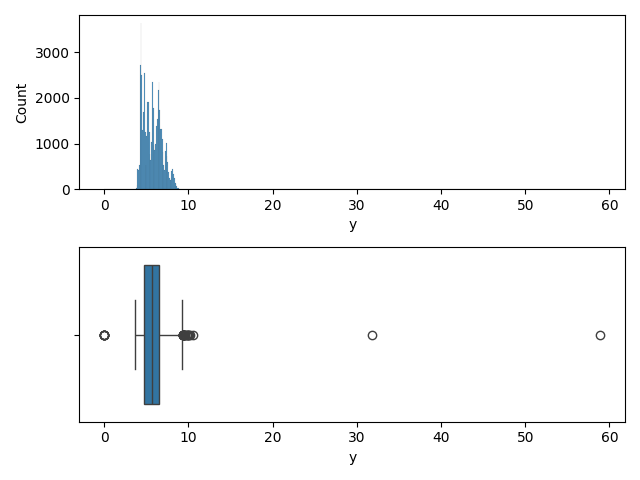
Variable 'y'
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='y', ax=ax[0])
sns.boxplot(data=df_numeric, x='y', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'y'
Des outliers et une allure Gaussienne => Standardisation
Des outliers et une allure Gaussienne => Standardisation
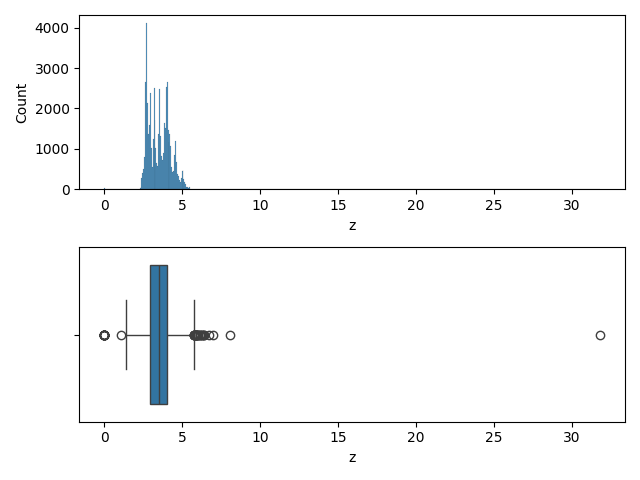
Variable 'z'
fig,ax = plt.subplots(2, 1)
sns.histplot(data=df_numeric, x='z', ax=ax[0])
sns.boxplot(data=df_numeric, x='z', ax=ax[1])
plt.tight_layout()

→
Conclusion pour la variable 'z'
Des outliers et une allure Gaussienne => Standardisation
Des outliers et une allure Gaussienne => Standardisation
4. Normalization MinMax
- convient pour la plupart des distributions
- à éviter pour les valeurs aberrantes
- à éviter pour les valeurs aberrantes
MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(df_numeric)
scaler.transform(df_numeric)
[[0.00623701 0.51388889 0.23076923 ... 0.36778399 0.06757216 0.07641509] [0.002079 0.46666667 0.34615385 ... 0.36219739 0.06519525 0.07264151] [0.00623701 0.38611111 0.42307692 ... 0.37709497 0.06910017 0.07264151] ... [0.1039501 0.55 0.32692308 ... 0.52700186 0.09643463 0.11194969] [0.13721414 0.5 0.28846154 ... 0.5726257 0.10390492 0.11761006] [0.11434511 0.53333333 0.23076923 ... 0.54283054 0.09966044 0.11446541]]
MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(df_numeric)
df_minmax = pd.dataFrame(scaler.transform(df_numeric), columns=df_numeric.columns)
carat depth table price x y z 0 0.006237 0.513889 0.230769 0.000000 0.367784 0.067572 0.076415 1 0.002079 0.466667 0.346154 0.000000 0.362197 0.065195 0.072642 2 0.006237 0.386111 0.423077 0.000054 0.377095 0.069100 0.072642 3 0.018711 0.538889 0.288462 0.000433 0.391061 0.071817 0.082704 4 0.022869 0.563889 0.288462 0.000487 0.404097 0.073854 0.086478 ... ... ... ... ... ... ... ... 53935 0.108108 0.494444 0.269231 0.131427 0.535382 0.097793 0.110063 53936 0.108108 0.558333 0.230769 0.131427 0.529795 0.097623 0.113522 53937 0.103950 0.550000 0.326923 0.131427 0.527002 0.096435 0.111950 53938 0.137214 0.500000 0.288462 0.131427 0.572626 0.103905 0.117610 53939 0.114345 0.533333 0.230769 0.131427 0.542831 0.099660 0.114465 [53940 rows x 7 columns]
df_minmax.describe()
carat depth ... y z count 53940.000000 53940.000000 ... 53940.000000 53940.000000 mean 0.124312 0.520817 ... 0.097360 0.111281 std 0.098547 0.039795 ... 0.019391 0.022192 min 0.000000 0.000000 ... 0.000000 0.000000 25% 0.041580 0.500000 ... 0.080136 0.091509 50% 0.103950 0.522222 ... 0.096944 0.111006 75% 0.174636 0.541667 ... 0.111036 0.127044 max 1.000000 1.000000 ... 1.000000 1.000000 [8 rows x 7 columns]
Comparatif df_numeric et df_minmax
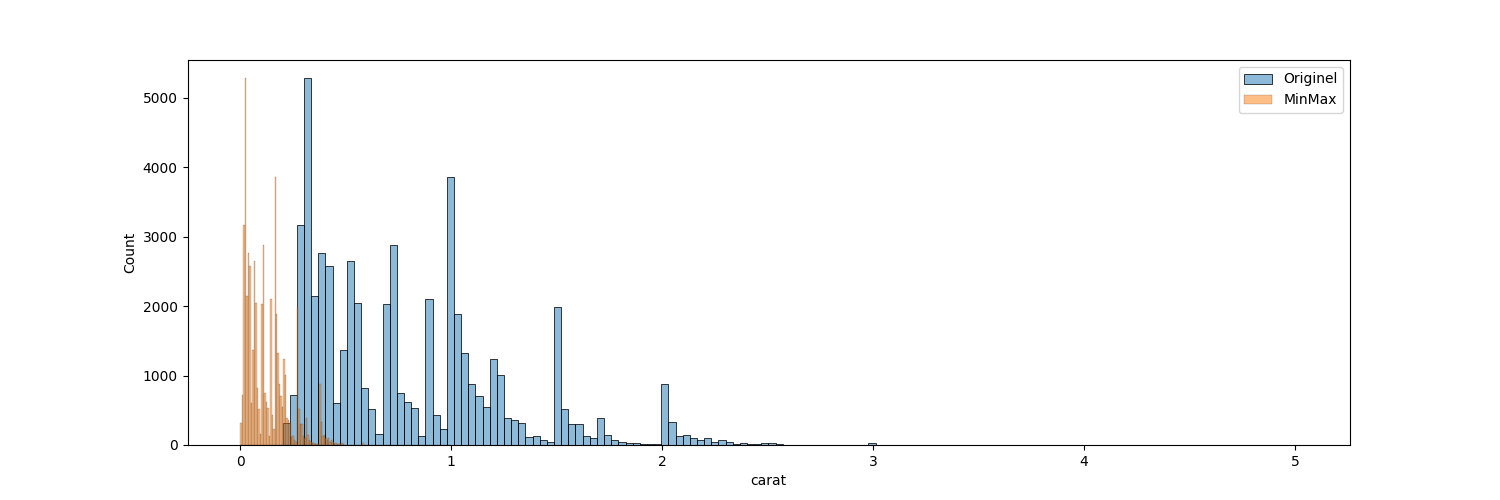
plt.figure(figsize=(15,5))
sns.histplot(data=df_numeric, x='carat', color='tab:blue', alpha=0.5)
sns.histplot(data=df_minmax, x='carat', color='tab:orange', alpha=0.5)

5. Standartisation
- Donne de bons résultats aux variables suivant une allure Gaussienne
StandardScaler
scaler = StandardScaler()
scaler.fit(df_numeric)
df_minmax = pd.dataFrame(scaler.transform(df_numeric), columns=df_numeric.columns)
carat depth table price x y z 0 0.006237 0.513889 0.230769 0.000000 0.367784 0.067572 0.076415 1 0.002079 0.466667 0.346154 0.000000 0.362197 0.065195 0.072642 2 0.006237 0.386111 0.423077 0.000054 0.377095 0.069100 0.072642 3 0.018711 0.538889 0.288462 0.000433 0.391061 0.071817 0.082704 4 0.022869 0.563889 0.288462 0.000487 0.404097 0.073854 0.086478 ... ... ... ... ... ... ... ... 53935 0.108108 0.494444 0.269231 0.131427 0.535382 0.097793 0.110063 53936 0.108108 0.558333 0.230769 0.131427 0.529795 0.097623 0.113522 53937 0.103950 0.550000 0.326923 0.131427 0.527002 0.096435 0.111950 53938 0.137214 0.500000 0.288462 0.131427 0.572626 0.103905 0.117610 53939 0.114345 0.533333 0.230769 0.131427 0.542831 0.099660 0.114465 [53940 rows x 7 columns]
df_standard.describe()
carat depth ... y z count 5.394000e+04 5.394000e+04 ... 5.394000e+04 5.394000e+04 mean 2.444878e-16 -3.996902e-15 ... -8.430615e-17 -2.002271e-16 std 1.000009e+00 1.000009e+00 ... 1.000009e+00 1.000009e+00 min -1.261458e+00 -1.308760e+01 ... -5.020931e+00 -5.014556e+00 25% -8.395232e-01 -5.231053e-01 ... -8.882800e-01 -8.909461e-01 50% -2.066210e-01 3.531678e-02 ... -2.147398e-02 -1.237618e-02 75% 5.106683e-01 5.239361e-01 ... 7.052421e-01 7.103184e-01 max 8.886075e+00 1.204139e+01 ... 4.654965e+01 4.004758e+01 [8 rows x 7 columns]
Comparatif df_numeric, df_minmax et df_standard (histogrammes)
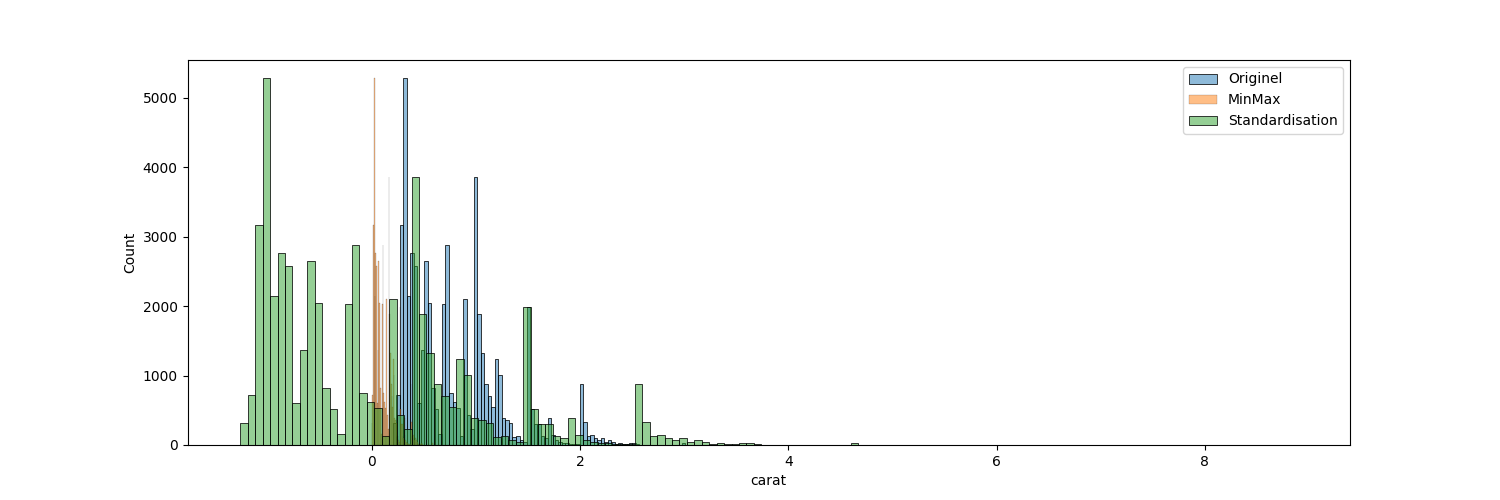
plt.figure(figsize=(15,5))
sns.histplot(data=df_numeric, x='carat', color='tab:blue', alpha=0.5)
sns.histplot(data=df_minmax, x='carat', color='tab:orange', alpha=0.5)
sns.histplot(data=df_standard, x='carat', color='tab:green', alpha=0.5)

Comparatif df_numeric, df_minmax et df_standard (Box plots)
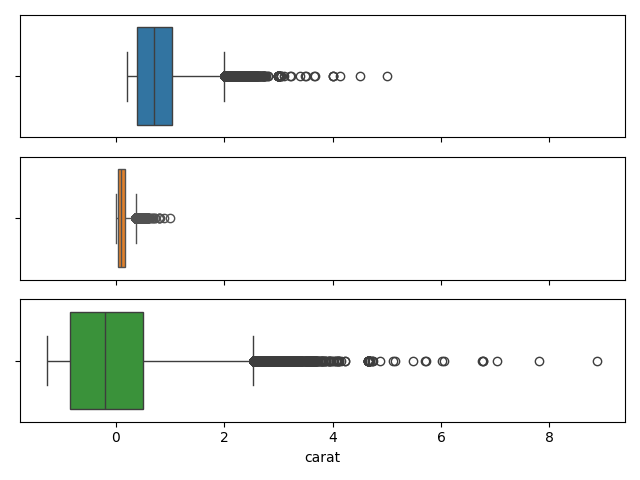
fig,ax = plt.subplots(3, 1, sharex=True)
sns.boxplot(data=df_numeric, x='carat', ax=ax[0], color='tab:blue')
sns.boxplot(data=df_minmax, x='carat', ax=ax[1], color='tab:orange')
sns.boxplot(data=df_standard, x='carat', ax=ax[2], color='tab:green')
plt.tight_layout()

→
Ni MinMax, ni Standardization => testons les deux