Health Expectancy - Tests d'Hypothèses
1. Spending_USD et Life_Expectancy semblent être corrélées.
2. Il semblait également que l'Allemagne et la Grande-Bretagne avaient la même durée de vie moyenne de 1970 à 2020.
3. Un politicien américain affirme que depuis 1970, la durée de vie aux États-Unis augmente en moyenne de 0,3 an.
2. Il semblait également que l'Allemagne et la Grande-Bretagne avaient la même durée de vie moyenne de 1970 à 2020.
3. Un politicien américain affirme que depuis 1970, la durée de vie aux États-Unis augmente en moyenne de 0,3 an.
1. Spending_USD et Life_Expectancy semblent être corrélées.
df_temp = df.query("`Year` <= 2020 & `Year` >= 2000 & `Country` == 'USA'")
Year Country Spending_USD Life_Expectancy 153 2000 USA 4536.561 76.7 159 2001 USA 4888.518 76.9 165 2002 USA 5316.522 77.0 171 2003 USA 5726.538 77.1 177 2004 USA 6069.530 77.6 183 2005 USA 6430.757 77.6 189 2006 USA 6808.054 77.8 195 2007 USA 7166.513 78.1 201 2008 USA 7385.026 78.1 207 2009 USA 7645.002 78.5 213 2010 USA 7879.253 78.6 219 2011 USA 8079.467 78.7 225 2012 USA 8346.064 78.8 231 2013 USA 8519.620 78.8 237 2014 USA 8925.879 78.9 243 2015 USA 9355.118 78.7 249 2016 USA 9717.649 78.7 255 2017 USA 10046.472 78.6 261 2018 USA 10451.386 78.7 267 2019 USA 10855.517 78.8 273 2020 USA 11859.179 77.0
df_temp = df.query("`Year` <= 2020 & `Year` >= 2000 & `Country` == 'USA'")
sns.scatterplot(data=df_temp, x='Spending_USD', y='Life_Expectancy')
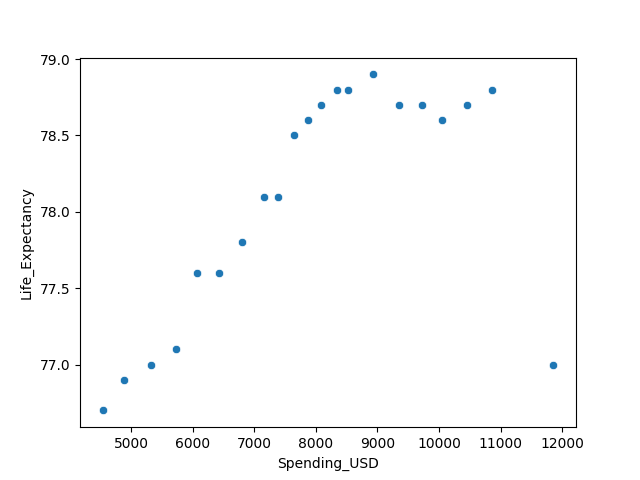
Question 1 : Quelle est la corrélation de Pearson entre ces deux variables aux États-Unis, de 2000 à 2020 ?
Test de Pearson
personr(df_temp['Spending_USD'], df_temp['Life_Expectancy'])
PearsonRResult(statistic=np.float64(0.6210674528998252), pvalue=np.float64(0.002658154480579906))
→
Le coefficient de corrélation de Pearson entre ces deux variables est de 0.62
(1= les deux variables augmentent ensemble, 0= pas de lien, -1=Une variable augmente quand l'autre diminue)
(1= les deux variables augmentent ensemble, 0= pas de lien, -1=Une variable augmente quand l'autre diminue)
Question 2 : Quelle serait la probabilité d'obtenir une corrélation au moins aussi importante que celle-ci, si en réalité les deux variables n'étaient pas corrélées ?
Nombre de chances d'obtenir ces résultats
p_value = personr(df_temp['Spending_USD'], df_temp['Life_Expectancy']).pvalue
1 / pvalue
376.20085939544
→
La probabilité d'obtenir une telle corrélation si les deux variables étaient en réalité totalement décorrélées serait de 0.0026
Autrement dit, elle serait de 1 chance sur 326
Autrement dit, elle serait de 1 chance sur 326
Nombre de chances d'obtenir cette corrélation
1 / ttest_1samp(df_temp, popmean=0.3).pvalue
1956.176463661705
2. Il semblait également que l'Allemagne et la Grande-Bretagne avaient la même durée de vie moyenne de 1970 à 2020.
df_temp = df.query("`Country` == 'Germany' | `Country` == 'Great Britain'")
sns.scatterplot(data=df_temp, x='Year', y='Life_Expectancy', hue='Country')
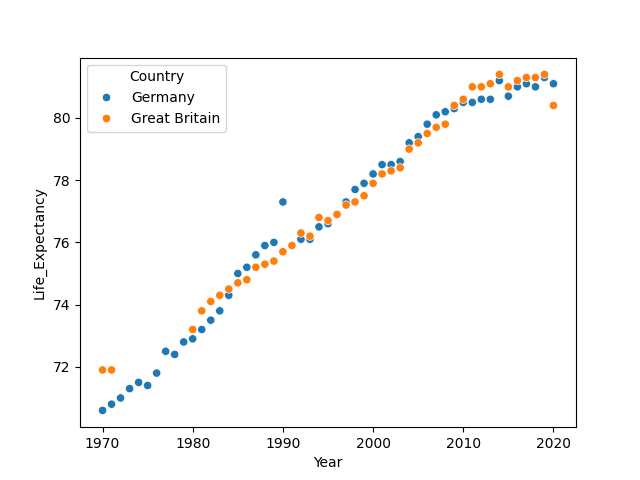
Test de Student ?
Non car il y a une dépendance entre les données (série temporelle).
Non car il compare seulement les moyennes, quelle que soit l'évolution. => Utiliser un modèle pour séries temporelles
Non car il y a une dépendance entre les données (série temporelle).
Non car il compare seulement les moyennes, quelle que soit l'évolution. => Utiliser un modèle pour séries temporelles
3. Un politicien américain affirme que depuis 1970, la durée de vie aux États-Unis augmente en moyenne de 0,3 an.
Différences de Life_Expectancy année après année.
df_temp = df.query("`Country` == 'USA'")['Life_Expectancy'].diff().dropna()
9 0.3 12 0.0 15 0.2 18 0.6 22 0.7 26 0.2 29 0.4 32 0.2 36 0.4 42 -0.2 47 0.4 52 0.4 57 0.1 62 0.1 68 0.0 73 0.0 78 0.2 83 0.0 88 0.2 94 0.2 99 0.2 105 0.2 111 -0.2 117 0.2 123 0.0 129 0.4 135 0.4 141 0.2 147 0.0 153 0.0 159 0.2 165 0.1 171 0.1 177 0.5 183 0.0 189 0.2 195 0.3 201 0.0 207 0.4 213 0.1 219 0.1 225 0.1 231 0.0 237 0.1 243 -0.2 249 0.0 255 -0.1 261 0.1 267 0.1 273 -1.8 Name: Life_Expectancy, dtype: float64
Statistiques des différences de Life_Expectancy année après année.
df_temp.describe()
count 50.000000 mean 0.122000 std 0.338237 min -1.800000 25% 0.000000 50% 0.100000 75% 0.200000 max 0.700000 Name: Life_Expectancy, dtype: float64
0.122 +/- 0.338 convient ?
Test de Student à 1 échantillon (ttest 1 sample).
ttest_1samp(df_temp, popmean=0.3)
TtestResult(statistic=np.float64(-3.7212105613188773), pvalue=np.float64(0.0005112013249193949), df=np.int64(49))
Données indépendantes les unes des autres : OK
Issues d'une distribution normale (ou bien plus de 30 points) : OK (51 points et distribution normale)
Issues d'une distribution normale (ou bien plus de 30 points) : OK (51 points et distribution normale)
→
La p_value de notre test est inférieure à 0.02 => On peut rejeter l'hypothèse du politicien américain
Une chance sur 1956 d'observer ces résultat là si le politicien avait raison avec une augmentation de 0.3 an chaque année
Une chance sur 1956 d'observer ces résultat là si le politicien avait raison avec une augmentation de 0.3 an chaque année