Miles Per Gallon - Analyze
1. Déterminez quelles sont les variables Discrètes et Continues du dataset
2. Analysez la variable 'mpg'
2. Analysez la variable 'cylinders'
4. Analysez la variable 'origin'
5. Analysez l’évolution de la consommation des voitures (mpg) par rapport à la puissance (horsepower)
6. Observez l’évolution du poids moyen (weight) des voitures américaines de l’année 70 jusqu’à l’année 82
7. Analysez la relation entre le nombre de cylindres et l’année du modèle
8. Analysez la relation entre le nombre de cylindres et l’origine
9. Quelle est l’accélération moyenne des voitures des différents pays ?
10. Quelle est-elle pour les modèles de l’année 80 ?
11. Au final? Il semblerait qu’une tendance se dégage à travers le temps...
2. Analysez la variable 'mpg'
2. Analysez la variable 'cylinders'
4. Analysez la variable 'origin'
5. Analysez l’évolution de la consommation des voitures (mpg) par rapport à la puissance (horsepower)
6. Observez l’évolution du poids moyen (weight) des voitures américaines de l’année 70 jusqu’à l’année 82
7. Analysez la relation entre le nombre de cylindres et l’année du modèle
8. Analysez la relation entre le nombre de cylindres et l’origine
9. Quelle est l’accélération moyenne des voitures des différents pays ?
10. Quelle est-elle pour les modèles de l’année 80 ?
11. Au final? Il semblerait qu’une tendance se dégage à travers le temps...
1. Déterminez quelles sont les variables Discrètes et Continues du dataset
df.info()
df.nunique()
mpg 129 cylinders 5 displacement 82 horsepower 93 weight 351 acceleration 95 model_year 13 origin 3 name 305 dtype: int64
df.head()
mpg cylinders displacement ... model_year origin name 0 18.0 8 307.0 ... 70 usa chevrolet chevelle malibu 1 15.0 8 350.0 ... 70 usa buick skylark 320 2 18.0 8 318.0 ... 70 usa plymouth satellite 3 16.0 8 304.0 ... 70 usa amc rebel sst 4 17.0 8 302.0 ... 70 usa ford torino [5 rows x 9 columns]
Variables discrètes: 'cylinders', 'model_year', 'origin' et 'name'
Variables continues: 'mpg', 'displacement', 'horsepower', 'weight' et 'acceleration'
Variables continues: 'mpg', 'displacement', 'horsepower', 'weight' et 'acceleration'
2. Analysez la variable 'mpg'
df['mpg'].describe()
count 398.000000 mean 23.514573 std 7.815984 min 9.000000 25% 17.500000 50% 23.000000 75% 29.000000 max 46.600000 Name: mpg, dtype: float64
/!\ Miles per Gallon est différent de la consommation
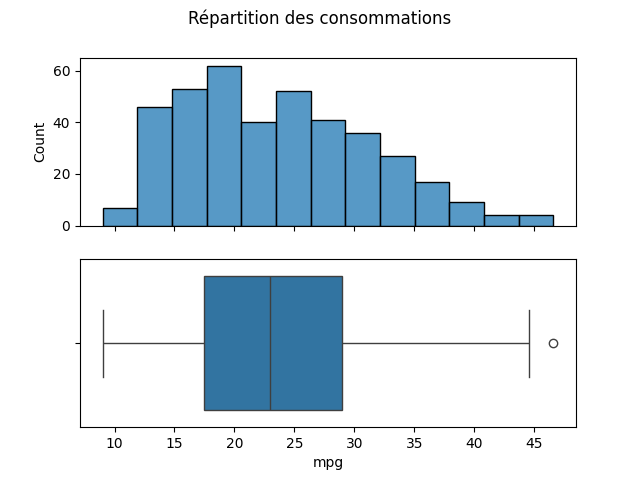
La consommation moyenne des voitures américaines, européennes et japonaises de 1970 à 1982 est de 23.5 mpg dans ce jeu de données (Source ?)
Avec un écart-type de 7.8 mpg
La consommation la plus élevée est de 9 mpg -> laquelle ?
La consommation la plus faible est de 46.6 mpg -> laquelle ?
La consommation moyenne des voitures américaines, européennes et japonaises de 1970 à 1982 est de 23.5 mpg dans ce jeu de données (Source ?)
Avec un écart-type de 7.8 mpg
La consommation la plus élevée est de 9 mpg -> laquelle ?
La consommation la plus faible est de 46.6 mpg -> laquelle ?
Quelle ligne pour 9 mpg ?
df.query("`mpg`== 9")
mpg cylinders displacement ... model_year origin name 28 9.0 8 304.0 ... 70 usa hi 1200d [1 rows x 9 columns]
→
Voiture américaine, année 1970, 8 cylindres, modèle 'hi 1200d'
Quelle ligne pour 46.6 mpg ?
df.query("`mpg`== 46.6")
mpg cylinders displacement ... model_year origin name 322 46.6 4 86.0 ... 80 japan mazda glc [1 rows x 9 columns]
→
Voiture japonaise, année 1980, modèle 'mazda glc'
fig, ax = sns.subplots(2, 1, sharex=True)
plt.suptitle('Répartition des consommations')
sns.histplot(data=df, x='mpg', ax=ax[0])
sns.boxplot(data=df, x='mpg', ax=ax[1])
2. Analysez la variable 'cylinders'
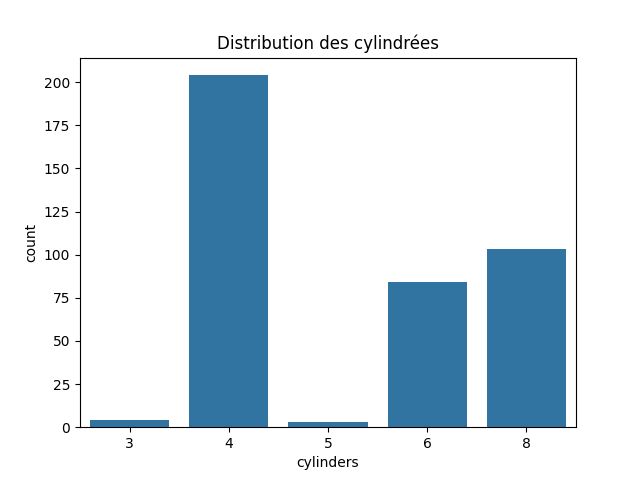
Distribution des cylindrées
df['cylinders'].value_counts(normalize=False)
cylinders 4 204 8 103 6 84 3 4 5 3 Name: count, dtype: int64
→
Il y a beaucoup de 4 cylindres parmi les modèles des années 70-82
Ensuite ce sont les 8 cylindres
Ensuite ce sont les 8 cylindres
sns.countplot(data=df, x='cylinders')
plt.title('Distribution des cylindrées')
4. Analysez la variable 'origin'
Distribution des origines
df['origin'].value_counts(normalize=False)
origin usa 249 japan 79 europe 70 Name: count, dtype: int64
→
Dans ce jeu de données, la majorité des modèles sont des américaines, et sinon il y a un nombre équivalent d’éuropéennes et de japonaises.
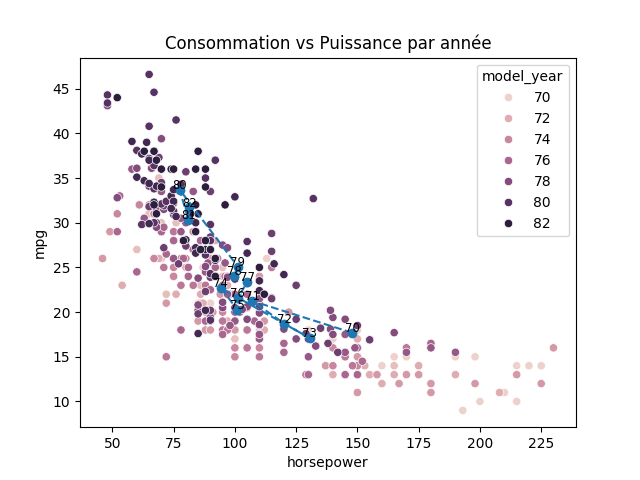
5. Analysez l’évolution de la consommation des voitures (mpg) par rapport à la puissance (horsepower)
sns.scatterplot(data=df, x='horsepower', y='mpg')
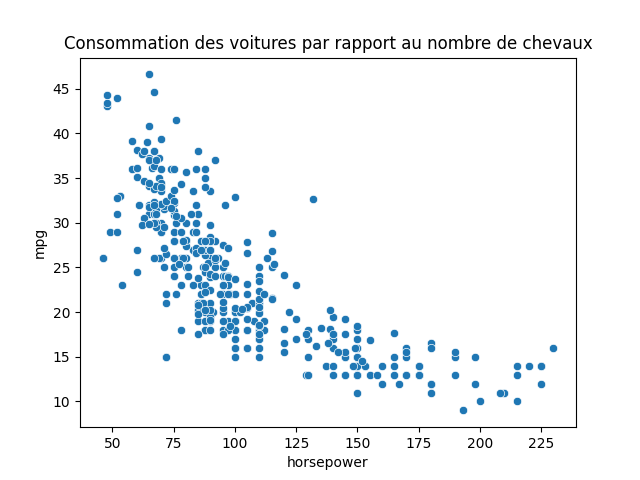
→
Les miles per Gallon diminuent lorsque que la puissance augmente.
<=> La consommation augmente lorsque que la puissance augmente.
Cette diminution n'est pas linéaire, mais suit une tendance quadratique
<=> La consommation augmente lorsque que la puissance augmente.
Cette diminution n'est pas linéaire, mais suit une tendance quadratique
sns.scatterplot(data=df, x='horsepower', y='mpg', hue='model_year')
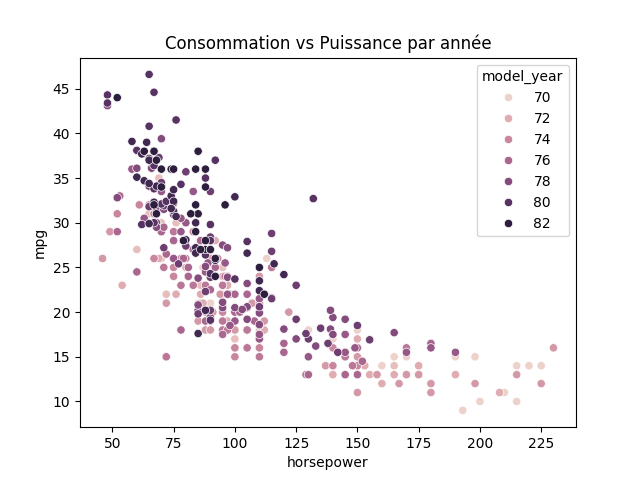
→
On observe qu'au cours du temps, les voitures consomment de moins en moins, et ont une puissance de plus en plus faible.
df.groupby('model_year')[['horsepower', 'mpg']].mean()
horsepower mpg model_year 70 147.827586 17.689655 71 107.037037 21.250000 72 120.178571 18.714286 73 130.475000 17.100000 74 94.230769 22.703704 75 101.066667 20.266667 76 101.117647 21.573529 77 105.071429 23.375000 78 99.694444 24.061111 79 101.206897 25.093103 80 77.481481 33.696552 81 81.035714 30.334483 82 81.466667 31.709677
sns.scatterplot(data=df, x='horsepower', y='mpg')
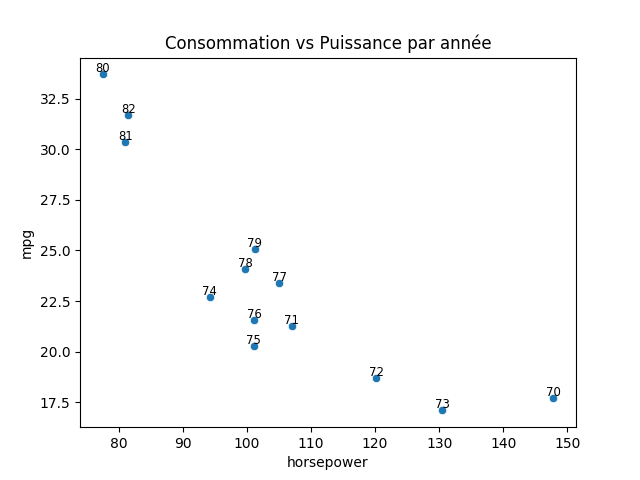
plt.plot(df_temp['horsepower'], df_temp['mpg'], '--o')
for index, row in df_temp.iterrows():
plt.text(row['horsepower'], row['mpg'] + 0.1, index, color='black', ha='center', size='small')
plt.xlabel('horsepower')
plt.ylabel('mpg')
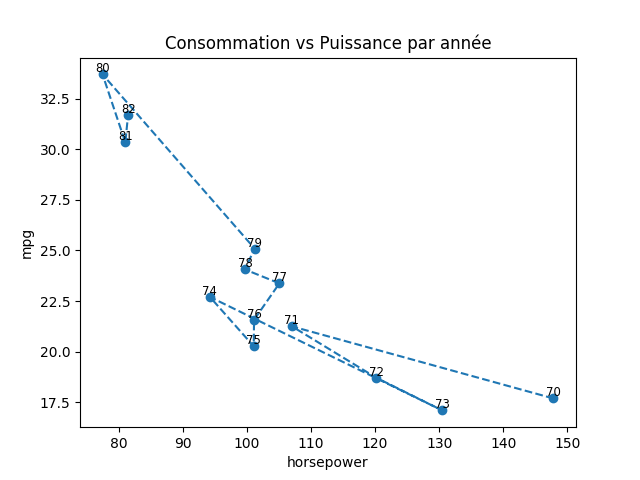
plt.plot(df_temp['horsepower'], df_temp['mpg'])
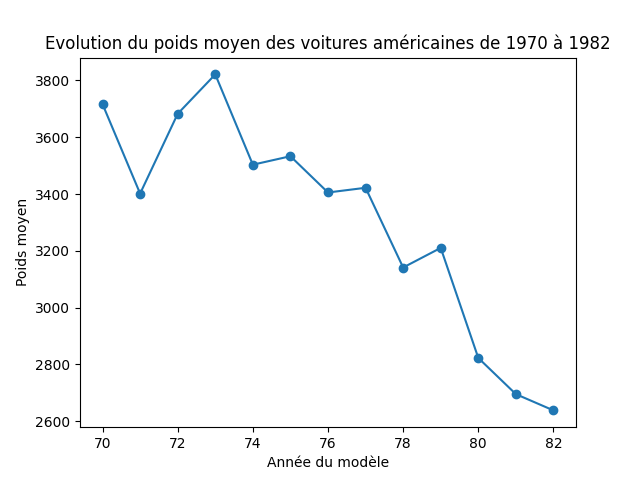
6. Observez l’évolution du poids moyen (weight) des voitures américaines de l’année 70 jusqu’à l’année 82
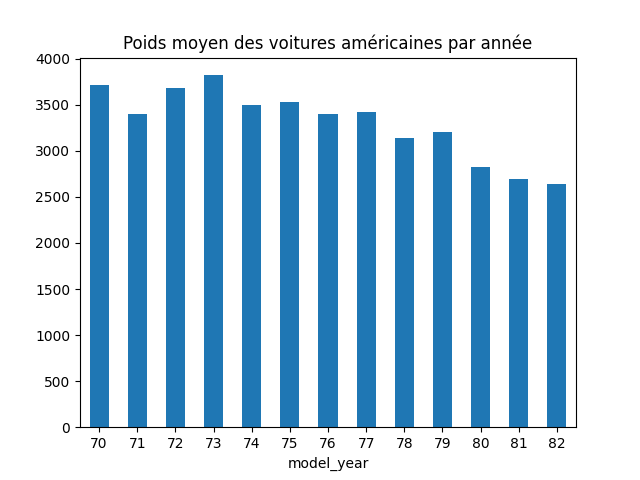
df.query("`origin`== 'usa'").groupby('model_year')['weight'].mean()
model_year 70 3716.500000 71 3401.600000 72 3682.666667 73 3821.448276 74 3503.333333 75 3533.200000 76 3405.409091 77 3422.000000 78 3141.136364 79 3210.217391 80 2822.428571 81 2695.000000 82 2637.750000 Name: weight, dtype: float64
→
Il semblerait que les voitures américaines soient de plus en plus légères.
df.query("`origin`== 'usa'").groupby('model_year')['weight'].mean().plot(kind='bar')
df_tmp = df.query("`origin`== 'usa'").groupby('model_year')['weight'].mean()
plt.plot(df_temp.index, df_temp.values)
data_plot = df.groupby(['origin', 'model_year'])['weight'].mean().reset_index()
sns.lineplot(data=data_plot, x='model_year', y='weight', hue='origin')
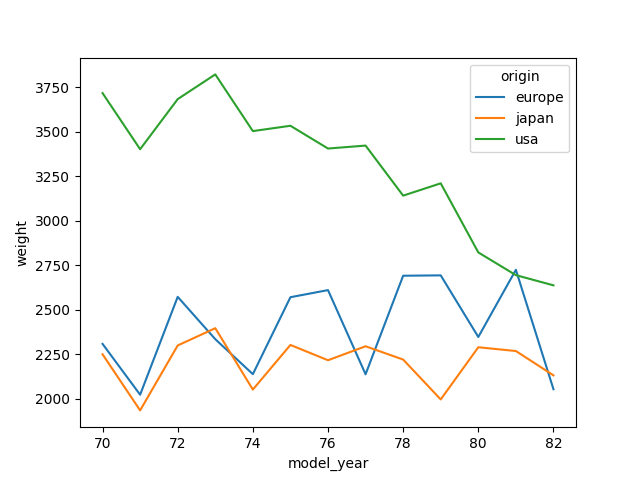
→
Les voitures sont de plus en plus légères aux USA, mais en Europe leur poids augmente légèrement. Au Japon, il reste le même
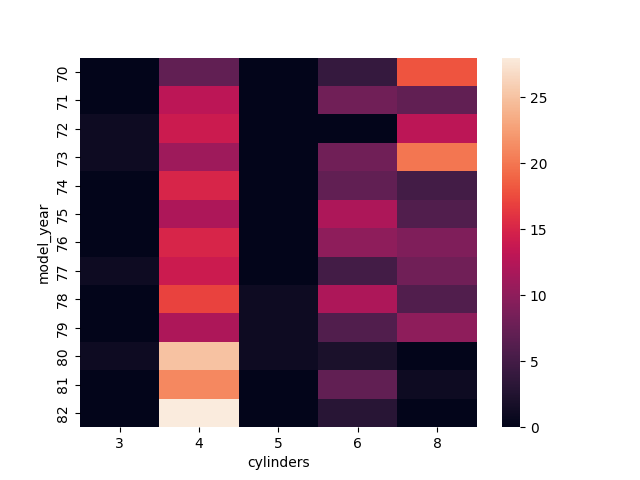
7. Analysez la relation entre le nombre de cylindres et l’année du modèle
Deux variables discrètes => table de contingence
pd.crosstab(df['model_year'], df['cylinders'])
cylinders 3 4 5 6 8 model_year 70 0 7 0 4 18 71 0 13 0 8 7 72 1 14 0 0 13 73 1 11 0 8 20 74 0 15 0 7 5 75 0 12 0 12 6 76 0 15 0 10 9 77 1 14 0 5 8 78 0 17 1 12 6 79 0 12 1 6 10 80 1 25 1 2 0 81 0 21 0 7 1 82 0 28 0 3 0
sns.heatmap(pd.crosstab(df['model_year'], df['cylinders']))
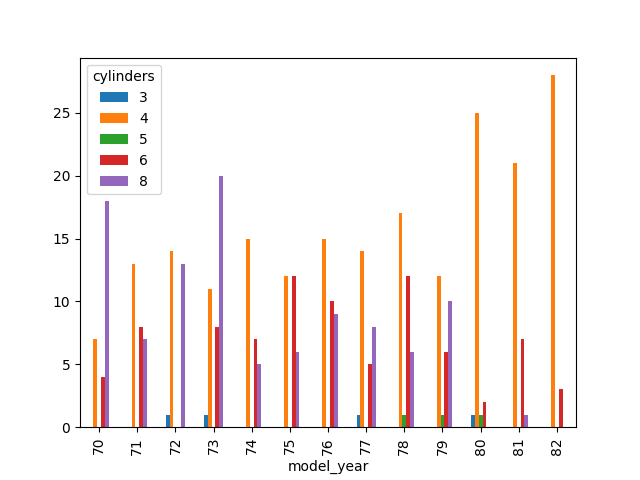
pd.crosstab(df['model_year'], df['cylinders'])).plot(kind='bar')
pd.crosstab(df['model_year'], df['cylinders'], normalize='index').plot(kind='bar', stacked=True)
plt.xlabel = 'Model Year'
plt.ylabel = 'Proportion'
plt.title('Proportion des cylindrées à travers les années')
plt.legend(title='cylinders', bbox_to_anchor=(1.05, 0), loc='lower right')
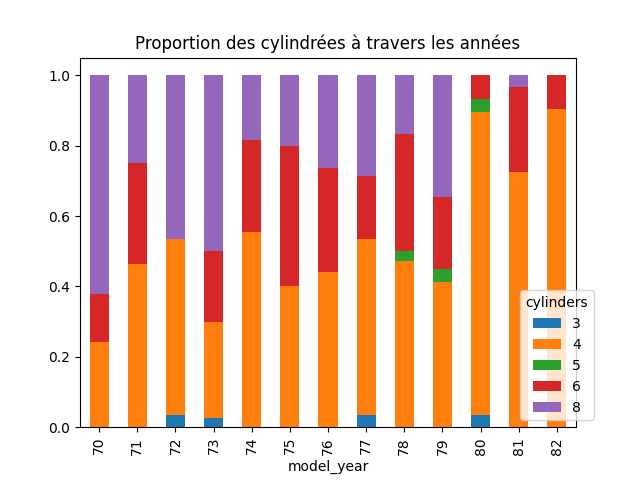
→
Sur l'ensemble de notre jeu de données, tout pays confondu, il semblerait qu'il y ait de moins en moins de 8 cylindres et de plus en plus de 4 cylindres
8. Analysez la relation entre le nombre de cylindres et l’origine
Deux variables discrètes => table de contingence
pd.crosstab(df['cylinders'], df['origin'])
origin europe japan usa cylinders 3 0 4 0 4 63 69 72 5 3 0 0 6 4 6 74 8 0 0 103
→
On observe (modèles de 1970 à 1982) que le nombre de véhicules de 4 cylindres est équivalent en Europe, au Japon et aux USA
Le Japon est le seul pays à avoir des 3 cylindres
L’Europe est le seul pays à avoir des 5 cylindres
Les USA sont les seuls à avoir des 8 cylindres
Les USA ont beaucoup plus de 5 cylindres qu’en Europe et au Japon
Le Japon est le seul pays à avoir des 3 cylindres
L’Europe est le seul pays à avoir des 5 cylindres
Les USA sont les seuls à avoir des 8 cylindres
Les USA ont beaucoup plus de 5 cylindres qu’en Europe et au Japon
9. Quelle est l’accélération moyenne des voitures des différents pays ?
df.groupby('origin')['acceleration'].mean()
origin europe 16.787143 japan 16.172152 usa 15.033735 Name: acceleration, dtype: float64
→
L'accélération moyenne des voitures semble être la même au Japon et en Europe, mais elle semble être plus faible aux USA
10. Quelle est-elle pour les modèles de l’année 80 ?
df.query("`model_year`== 80").groupby('origin')['acceleration'].mean()
origin europe 18.366667 japan 16.015385 usa 16.800000 Name: acceleration, dtype: float64
11. Au final? Il semblerait qu’une tendance se dégage à travers le temps...
Evolution des Miles per Gallon au cours du temps
df.groupby('model_year')['mpg'].mean()
model_year 70 17.689655 71 21.250000 72 18.714286 73 17.100000 74 22.703704 75 20.266667 76 21.573529 77 23.375000 78 24.061111 79 25.093103 80 33.696552 81 30.334483 82 31.709677 Name: mpg, dtype: float64
df.groupby('model_year')['mpg'].mean().plot()
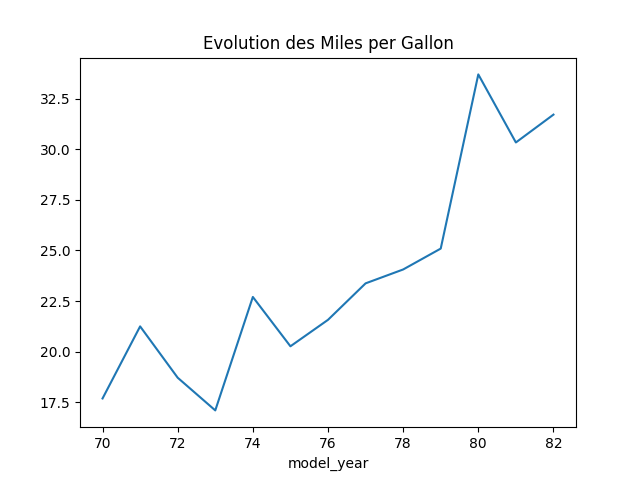
→
L’autonomie moyenne des voitures augmente au cours du temps
df_temp = df.groupby(['model_year', 'origin'])['mpg'].mean().reset_index()
sns.lineplot(df_temp, x='model_year', y='mpg', hue='origin')
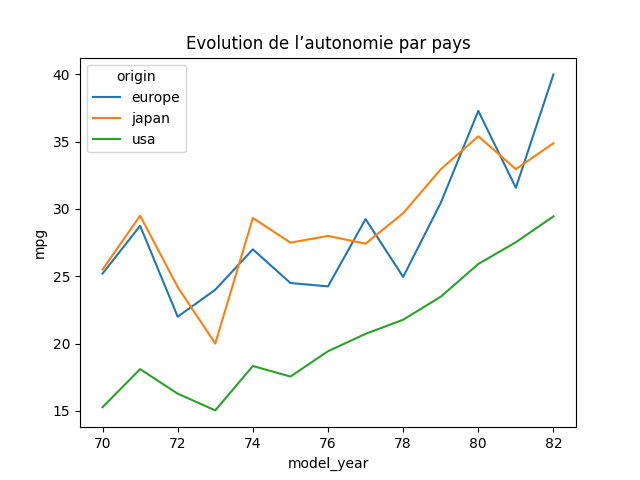
→
L’autonomie moyenne des voitures augmente au cours du temps, quel que soit le pays
df_temp = df.groupby(['model_year', 'cylinders'])['mpg'].mean().reset_index()
sns.lineplot(df_temp, x='model_year', y='mpg', hue='cylinders')
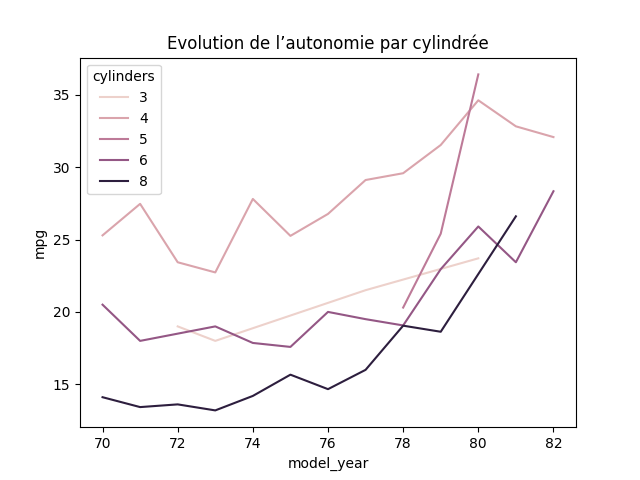
→
L’autonomie moyenne des voitures augmente au cours du temps, quel que soit la cylindrée
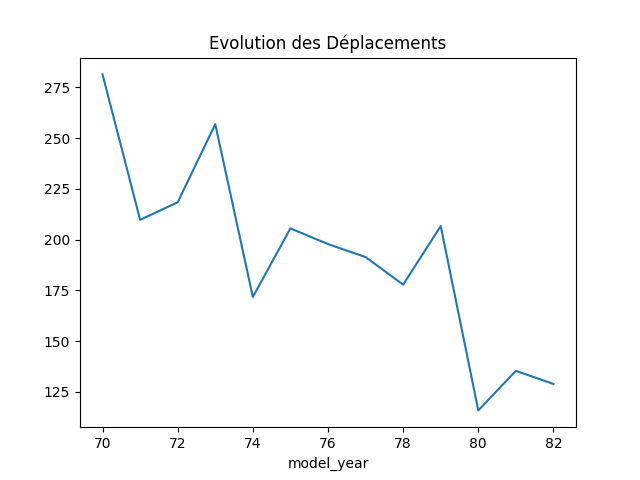
Evolution des Déplacements au cours du temps
df.groupby('model_year')['displacement'].mean()
model_year 70 281.413793 71 209.750000 72 218.375000 73 256.875000 74 171.740741 75 205.533333 76 197.794118 77 191.392857 78 177.805556 79 206.689655 80 115.827586 81 135.310345 82 128.870968 Name: displacement, dtype: float64
df.groupby('model_year')['displacement'].mean().plot()
→
Les déplacements moyens diminuent au cours du temps
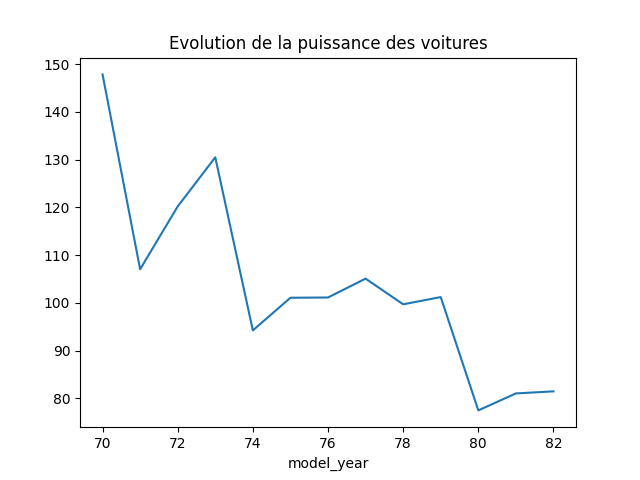
Evolution de la puissance des voitures au cours du temps
df.groupby('model_year')['horsepower'].mean()
model_year 70 147.827586 71 107.037037 72 120.178571 73 130.475000 74 94.230769 75 101.066667 76 101.117647 77 105.071429 78 99.694444 79 101.206897 80 77.481481 81 81.035714 82 81.466667 Name: horsepower, dtype: float64
df.groupby('model_year')['horsepower'].mean().plot()
→
La puissance moyenne des voitures diminue au cours du temps
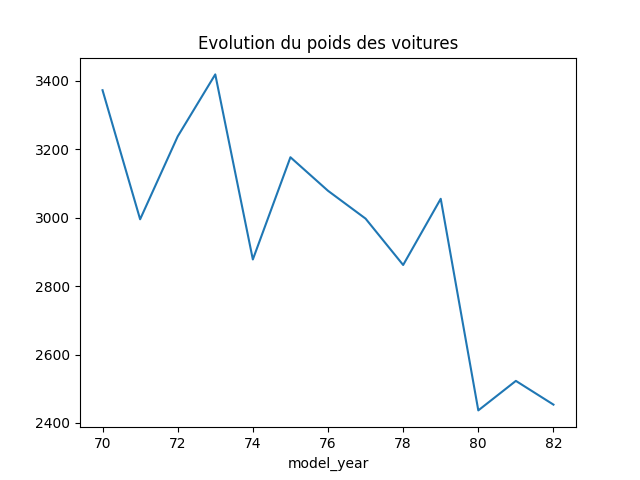
Evolution du poids des voitures au cours du temps
df.groupby('model_year')['weight'].mean()
model_year 70 3372.793103 71 2995.428571 72 3237.714286 73 3419.025000 74 2877.925926 75 3176.800000 76 3078.735294 77 2997.357143 78 2861.805556 79 3055.344828 80 2436.655172 81 2522.931034 82 2453.548387 Name: weight, dtype: float64
df.groupby('model_year')['weight'].mean().plot()
→
Le poids moyen des voitures diminue au cours du temps
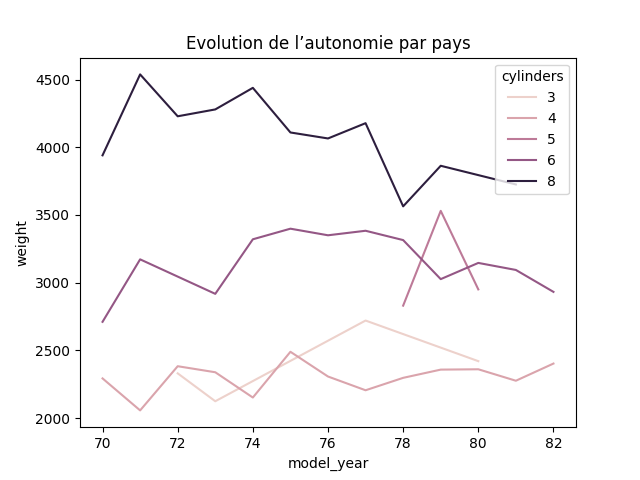
df_temp = df.groupby(['model_year', 'cylinders'])['weight'].mean().reset_index()
sns.lineplot(df_temp, x='model_year', y='weight', hue='cylinders')
→
Pas de tendance claire par cylindrée
Evolution de l'accélération des voitures au cours du temps
df.groupby('model_year')['acceleration'].mean()
model_year 70 12.948276 71 15.142857 72 15.125000 73 14.312500 74 16.203704 75 16.050000 76 15.941176 77 15.435714 78 15.805556 79 15.813793 80 16.934483 81 16.306897 82 16.638710 Name: acceleration, dtype: float64
df.groupby('model_year')['acceleration'].mean().plot()
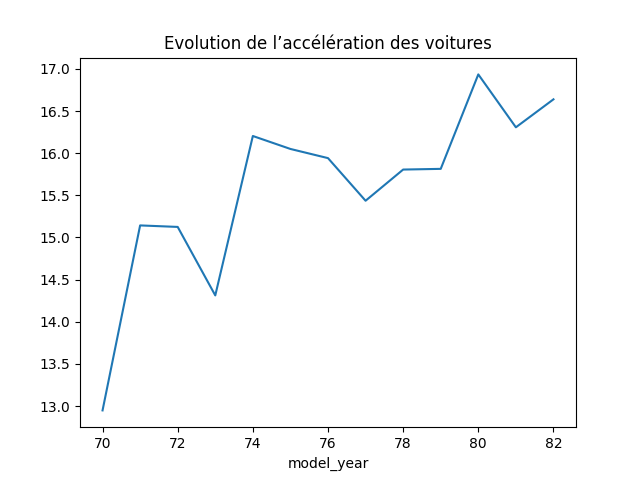
→
L’accélération moyenne des voitures augmente au cours du temps