Tips - Hypothesis

1. Variables discrètes - Tester une hypothèse avec un Test binomial
2. Variables discrètes - Tester une hypothèse avec un Test du Chi2
3. Variables continue - Tester une hypothèse avec un Test de Student (1 échantillon)
4. Deux variables discrètes - Tester une hypothèse avec un Test du Chi2 d’indépendance)
5. Deux groupes indépendants (dicrètes et continues) - Tester une hypothèse avec un Test de Student
6. Deux (ou plus) groupes indépendants (dicrètes et continues) - Tester une hypothèse avec ANOVA (Analysis of variance)
7. Deux variables continues - Tester une hypothèse de corrélation avec Pearson



1. Variables discrètes - Tester une hypothèse avec un Test binomial

Hypothèse 0
H0: 80% des pourboires sont donnés le soir

Enquête de terrain (value counts)
df['time'].value_counts(normalize=False, sort=True, ascending=False)

time
Dinner    176
Lunch      68
Name: count, dtype: int64

Enquête de terrain (percent)
df['time'].value_counts(normalize=True, sort=True, ascending=False)

time
Dinner    0.721311
Lunch     0.278689
Name: proportion, dtype: float64

P-Value
Probabilité d'observer une différence au moins aussi extrème si H0 est vraie
⇒ p = 0.8

Nombre d'essais réalisés
n = len(df)

244

Nombre de succès obtenus
k = df['time'].value_counts()['Dinner']

176

Tester l'hypothèse
p = 0.8
k = df['time'].value_counts()['Dinner']
n = len(df)
binomtest(k=k, n=n, p=p)

BinomTestResult(k=176, n=244, alternative='two-sided', statistic=0.7213114754098361, pvalue=0.002988997747005771)

Conclusion
alpha = 0.02
p = 0.8
k = df['time'].value_counts()['Dinner']
n = len(df)
p_value = binomtest(k=k, n=n, p=p).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.002988997747005771
p_value < alpha
    Nous avons suffisament d’évidences pour rejeter H0


Test Binomial
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.binomtest.html




2. Variables discrètes - Tester une hypothèse avec un Test du Chi2

Hypothèse 0
H0: Les clients donnent des pourboires: 20% le jeudi, 10% le vendredi, 40% le samedi et 30% le dimanche
expected_frequencies = np.array([0.2, 0.1, 0.4, 0.3])

Enquête de terrain (value counts)
df['day'].value_counts(normalize=False, sort=False)

day
Thur    62
Fri     19
Sat     87
Sun     76
Name: count, dtype: int64

Nombre de mesures
len(df)

244

Enquête de terrain (percent)
df['day'].value_counts(normalize=True, sort=False).round(2)

day
Thur    0.25
Fri     0.08
Sat     0.36
Sun     0.31
Name: proportion, dtype: float64

Probabilités → Effectifs
expected_frequencies = np.array(0.2, 0.1, 0.4, 0.3)
expected_frequencies = expected_frequencies * len(df)

[48.8 24.4 97.6 73.2]

Enquête de terrain (value counts)
observed_frequencies = df['day'].value_counts(normalize=True, sort=False).round(2)

day
Thur    62
Fri     19
Sat     87
Sun     76
Name: count, dtype: int64

Chisquare
p_value = chisquare(f_obs=observed_frequencies, f_exp=expected_frequencies)

Power_divergenceResult(statistic=np.float64(6.023907103825136), pvalue=np.float64(0.11045286802428235))

Conclusion
alpha = 0.02
f_exp = np.array([0.2, 0.1, 0.4, 0.3]) * len(df)
f_obs = df['day'].value_counts(normalize=False, sort=False).round(2).values
p_value = chisquare(f_obs=observed_frequencies, f_exp=expected_frequencies).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.11045286802428235
p_value ≥ alpha ⇒ 
Nous n’avons pas suffisament d’évidences pour rejeter H0


Test du Chi2
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chisquare.html




3. Variables continue - Tester une hypothèse avec un Test de Student (1 échantillon)

Hypothèse 0
H0: Le pourboire moyen dans ce restaurant est de 3,50 USD

Enquête de terrain (value counts)
df['tip'].describe()

count    244.000000
mean       2.998279
std        1.383638
min        1.000000
25%        2.000000
50%        2.900000
75%        3.562500
max       10.000000
Name: tip, dtype: float64

Enquête de terrain : moyenne et écart type
Moyenne: df['tip'].mean() : 2.99827868852459
Ecart type: df['tip'].std() : 1.3836381890011822

Chisquare
ttest_1samp(df['tip'], popmean=3.5)

TtestResult(statistic=np.float64(-5.664152292840388), pvalue=np.float64(4.1605377123077016e-08), df=np.int64(243))

Conclusion
alpha = 0.02
p_value = ttest_1samp(df['tip'], popmean=3.5).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 4.1605377123077016e-08
p_value < alpha
    Nous avons suffisament d’évidences pour rejeter H0


Test de Student (1 échantillon)
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_1samp.html




4. Deux variables discrètes - Tester une hypothèse avec un Test du Chi2 d’indépendance)

Hypothèse 0
H0: Le nombre de personnes (size) et le jour de la semaine (day) sont 2 variables indépendantes l’une de l’autre
alpha=0.02

Enquête de terrain
df.head()

   total_bill   tip     sex smoker  day    time  size
0       16.99  1.01  Female     No  Sun  Dinner     2
1       10.34  1.66    Male     No  Sun  Dinner     3
2       21.01  3.50    Male     No  Sun  Dinner     3
3       23.68  3.31    Male     No  Sun  Dinner     2
4       24.59  3.61  Female     No  Sun  Dinner     4

Enquête de terrain (table de contingence)
pd.crosstab(df['size'], df['day'])

day   Thur  Fri  Sat  Sun
size                     
1        1    1    2    0
2       48   16   53   39
3        4    1   18   15
4        5    1   13   18
5        1    0    1    3
6        3    0    0    1

Chi2 Contingency
contingency_table = pd.crosstab(df['size'], df['day'])
chi2_contingency(contingency_table)

Chi2ContingencyResult(statistic=np.float64(29.632849936919712), pvalue=np.float64(0.013316478351860587), dof=15, expected_freq=array([[ 1.01639344,  0.31147541,  1.42622951,  1.24590164],
       [39.63934426, 12.14754098, 55.62295082, 48.59016393],
       [ 9.6557377 ,  2.95901639, 13.54918033, 11.83606557],
       [ 9.40163934,  2.88114754, 13.19262295, 11.52459016],
       [ 1.2704918 ,  0.38934426,  1.78278689,  1.55737705],
       [ 1.01639344,  0.31147541,  1.42622951,  1.24590164]]))

résultat → Dataframe
dataframe = pd.DataFrame(
    chi2_contingency(contingency_table).expected_freq,
    columns = df['day'].sort_values().unique(),
    index = df['size'].sort_values().unique()
).round()

   Thur   Fri   Sat   Sun
1   1.0   0.0   1.0   1.0
2  40.0  12.0  56.0  49.0
3  10.0   3.0  14.0  12.0
4   9.0   3.0  13.0  12.0
5   1.0   0.0   2.0   2.0
6   1.0   0.0   1.0   1.0

Conclusion
alpha = 0.02
p_value = chi2_contingency(contingency_table).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.013316478351860587
p_value < alpha
    Nous avons suffisament d’évidences pour rejeter H0


Affichage différences
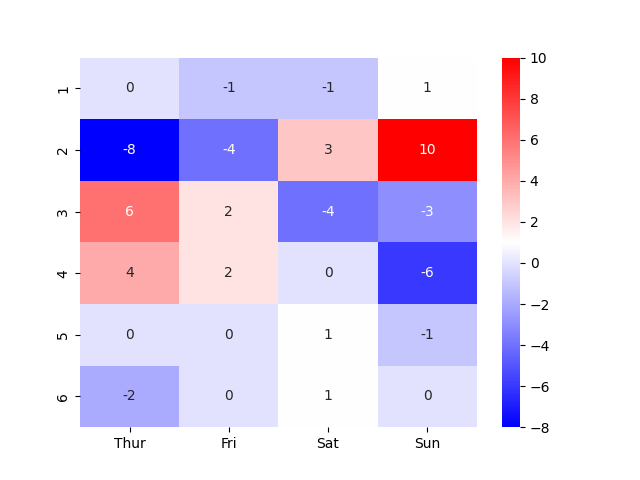
diff = dataframe - contingency_table
sns.heatmap(diff, annot=True, cmap='bwr')

Test du Chi2 d’indépendance
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html




5. Deux groupes indépendants (dicrètes et continues) - Tester une hypothèse avec un Test de Student

Conditions pour utiliser un test de Student à 2 groupes
- Les données doivent être indépendantes
- Les données doivent être identiquement distribuées
- Les données doivent suivre une Loi normale ou il doit y avoir plus de 30 points dans chaquie groupe (TCL - Théorème Central Limite)
Remarque : equal_var : bool, optional. False => Welch’s t-test si pas la même variance.

Hypothèse 0
Teste si deux moyennes sont identiques entre 2 groupes
H0: Les hommes donnent en moyenne le même pourboire que les femmes
alpha = 0.02

Enquête de terrain
df.groupby('sex')['tip'].describe()

        count      mean       std  min  25%   50%   75%   max
sex                                                          
Male    157.0  3.089618  1.489102  1.0  2.0  3.00  3.76  10.0
Female   87.0  2.833448  1.159495  1.0  2.0  2.75  3.50   6.5

On sépare les deux dataframes
df_male = df.query("sex == 'Male'")
df_female = df.query("sex == 'Female'")
result = ttest_ind(df_male['tips'], df_female['tips'])

TtestResult(statistic=np.float64(1.387859705421269), pvalue=np.float64(0.16645623503456755), df=np.float64(242.0))

Conclusion
alpha = 0.02
p_value = ttest_ind(df_male['tip'], df_female['tip']).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.16645623503456755
p_value ≥ alpha ⇒ 
Nous n’avons pas suffisament d’évidences pour rejeter H0


Test de Student (2 échantillons indépendants)
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html




6. Deux (ou plus) groupes indépendants (dicrètes et continues) - Tester une hypothèse avec ANOVA (Analysis of variance)

Hypothèse 0
Teste si deux moyennes sont identiques entre 2 groupes ou plus
H0: Le pourboire est le même en moyenne tous les jours
alpha = 0.02

Enquête de terrain
df.groupby('day')['tip'].mean()

day
Thur    2.771452
Fri     2.734737
Sat     2.993103
Sun     3.255132
Name: tip, dtype: float64

Enquête de terrain
df.groupby('day')['tip'].apply(list)

day
Thur    [4.0, 3.0, 2.71, 3.0, 3.4, 1.83, 5.0, 2.03, 5....
Fri     [3.0, 3.5, 1.0, 4.3, 3.25, 4.73, 4.0, 1.5, 3.0...
Sat     [3.35, 4.08, 2.75, 2.23, 7.58, 3.18, 2.34, 2.0...
Sun     [1.01, 1.66, 3.5, 3.31, 3.61, 4.71, 2.0, 3.12,...
Name: tip, dtype: object

Test ANOVA
f_oneway(*df.groupby('day')['tip'].apply(list))

F_onewayResult(statistic=np.float64(1.6723551980998699), pvalue=np.float64(0.1735885553040592))

Conclusion
alpha = 0.02
p_value = ttest_ind(df_male['tip'], df_female['tip']).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.1735885553040592
p_value ≥ alpha ⇒ 
Nous n’avons pas suffisament d’évidences pour rejeter H0


ANOVA (Analysis Of Variance)
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.f_oneway.html




7. Deux variables continues - Tester une hypothèse de corrélation avec Pearson

Hypothèse 0
Teste s'il existe une corrélation entre 2 variables continues
H0: Le pourboire n'est pas correlé au montant de l'addition
alpha = 0.02

Enquête de terrain
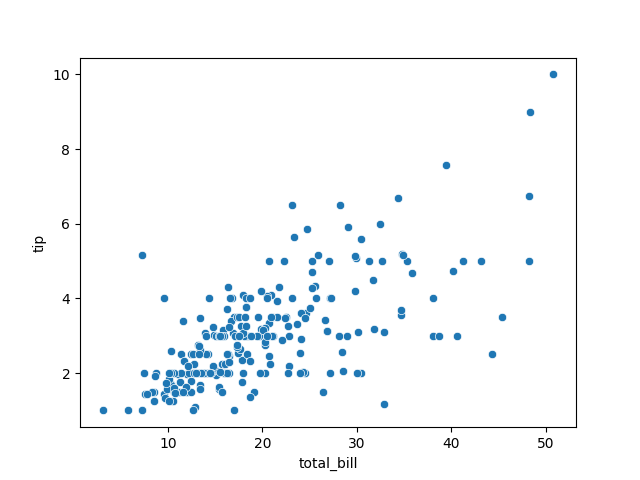
sns.scatterplot(data=df, x='total_bill', y='tip')

Test Pearson
pearsonr(df['total_bill'], df['tip'])

PearsonRResult(statistic=np.float64(0.6757341092113645), pvalue=np.float64(6.692470646863728e-34))

Conclusion
alpha = 0.02
p_value = ttest_ind(df_male['tip'], df_female['tip']).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 6.692470646863728e-34
p_value < alpha
    Nous avons suffisament d’évidences pour rejeter H0


Enquête de terrain
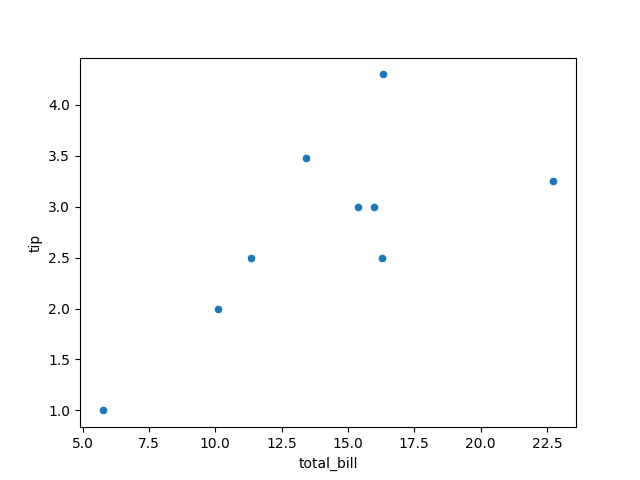
sns.scatterplot(data=df_female_friday, x='total_bill', y='tip')

Test Pearson
pearsonr(df_female_friday['total_bill'], df['tip'])

PearsonRResult(statistic=np.float64(0.7176682991060548), pvalue=np.float64(0.02948261189502928))

Conclusion
alpha = 0.02
p_value = ttest_ind(df_male['tip'], df_female['tip']).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.02948261189502928
p_value ≥ alpha ⇒ 
Nous n’avons pas suffisament d’évidences pour rejeter H0


Test de Pearson
 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pearsonr.html