Miles Per Gallon - Hypothesis
1. Analysez l’évolution de la consommation des voitures (mpg) par rapport à la puissance du moteur
2. Peut-on affirmer avec un risque d'erreur de 2% que les voitures du Japon, d'Europe, et des États-Unis ont vu leur autonomie moyenne (mpg) augmenter entre la premiere moitiée des années 70s et la seconde moitiée des années 70s ?
3. Un constructeur automobile américain affirme que les voitures américaines à 4 cylindres ont en moyenne la même accélération que les voitures américaines à 6 cylindres. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02).
4. Un collectionneur de voitures affirme que parmi les voitures Ford des années 1970-1982, il y a 25% de 4 cylindres, 25% de 6 cylindres et 50% de 8 cylindres. Testez son affirmation et concluez avec un niveau de confiance de 98%.
5. Les voitures à 4 cylindres ont en moyenne la même consommation d'essence au Japon, en Europe et aux États-Unis, dans les années 1970-1982. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02).
6. Les voitures européennes et japonaises ont en moyenne le même nombre de chevaux. Testez cette affirmation et concluez avec un niveau de confiance de 98 % (alpha = 0,02).
7. Un spécialiste vous dit que les constructeurs Ford et Dodge produisaient dans les années 70-82 des voitures avec un nombre de cylindres équivalent. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02)
2. Peut-on affirmer avec un risque d'erreur de 2% que les voitures du Japon, d'Europe, et des États-Unis ont vu leur autonomie moyenne (mpg) augmenter entre la premiere moitiée des années 70s et la seconde moitiée des années 70s ?
3. Un constructeur automobile américain affirme que les voitures américaines à 4 cylindres ont en moyenne la même accélération que les voitures américaines à 6 cylindres. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02).
4. Un collectionneur de voitures affirme que parmi les voitures Ford des années 1970-1982, il y a 25% de 4 cylindres, 25% de 6 cylindres et 50% de 8 cylindres. Testez son affirmation et concluez avec un niveau de confiance de 98%.
5. Les voitures à 4 cylindres ont en moyenne la même consommation d'essence au Japon, en Europe et aux États-Unis, dans les années 1970-1982. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02).
6. Les voitures européennes et japonaises ont en moyenne le même nombre de chevaux. Testez cette affirmation et concluez avec un niveau de confiance de 98 % (alpha = 0,02).
7. Un spécialiste vous dit que les constructeurs Ford et Dodge produisaient dans les années 70-82 des voitures avec un nombre de cylindres équivalent. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02)
1. Analysez l’évolution de la consommation des voitures (mpg) par rapport à la puissance du moteur
df.info()
df.nunique()
mpg 129 cylinders 5 displacement 82 horsepower 93 weight 351 acceleration 95 model_year 13 origin 3 name 305 dtype: int64
df.head()
mpg cylinders displacement ... model_year origin name 0 18.0 8 307.0 ... 70 usa chevrolet chevelle malibu 1 15.0 8 350.0 ... 70 usa buick skylark 320 2 18.0 8 318.0 ... 70 usa plymouth satellite 3 16.0 8 304.0 ... 70 usa amc rebel sst 4 17.0 8 302.0 ... 70 usa ford torino [5 rows x 9 columns]
sns.scatterplot(data=df, x='horsepower', y='mpg')
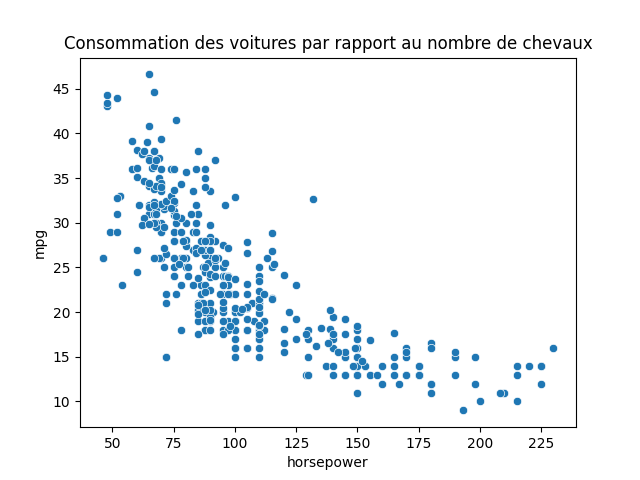
Corrélation de Pearson entre ces deux variables
pearsonr(x=df['horsepower'], y=df['mpg'])
PearsonRResult(statistic=np.float64(nan), pvalue=np.float64(nan))
→
La corrélation de pearson est de -0.778
Ces deux variables évoluent de manière significatives dans des directions oppsées.
Quand horse power augmente, mpg diminue.
Ces deux variables évoluent de manière significatives dans des directions oppsées.
Quand horse power augmente, mpg diminue.
→
La p-value est extrèmemeent faible : 7e-81
Il est impensable de dire que ces deux variables sont décorrelées
Il est impensable de dire que ces deux variables sont décorrelées
2. Peut-on affirmer avec un risque d'erreur de 2% que les voitures du Japon, d'Europe, et des États-Unis ont vu leur autonomie moyenne (mpg) augmenter entre la premiere moitiée des années 70s et la seconde moitiée des années 70s ?
sns.boxplot(data=df, x='model_year', y='mpg')
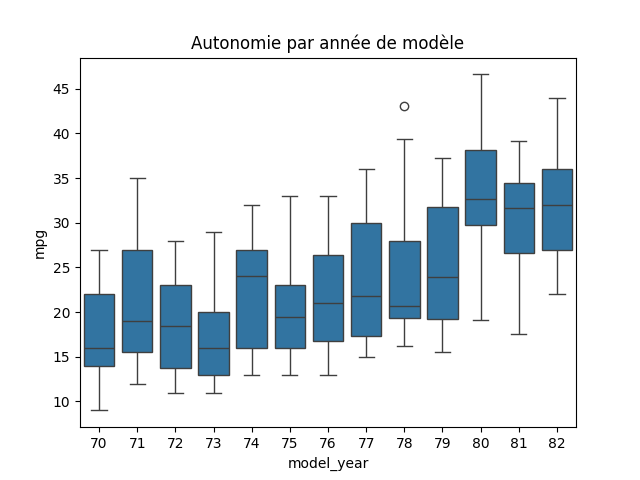
df_temp = df.copy()
df_temp['half'] = df['model_year'].apply(lambda x: x < 75).replace({True: 'first', False: 'second'})
df_temp = df_temp.query("`model_year` <= 80")
0 first
1 first
2 first
3 first
4 first
...
333 second
334 second
335 second
336 second
337 second
Name: half, Length: 338, dtype: object
sns.boxplot(data=df_temp, x='model_year', y='mpg', hue='half')
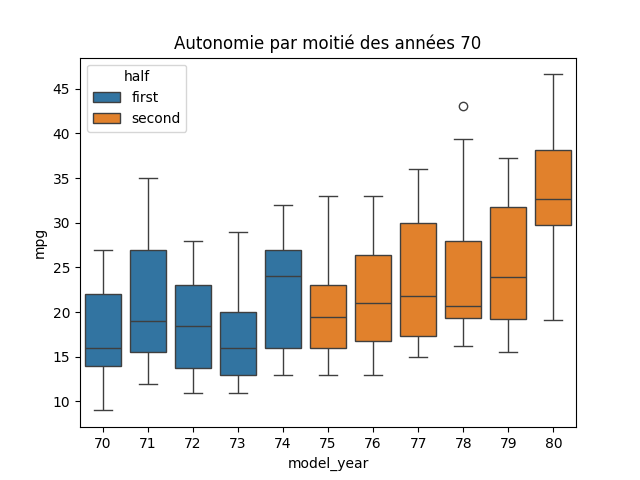
sns.boxplot(data=df_temp, x='half', y='mpg', hue='half')
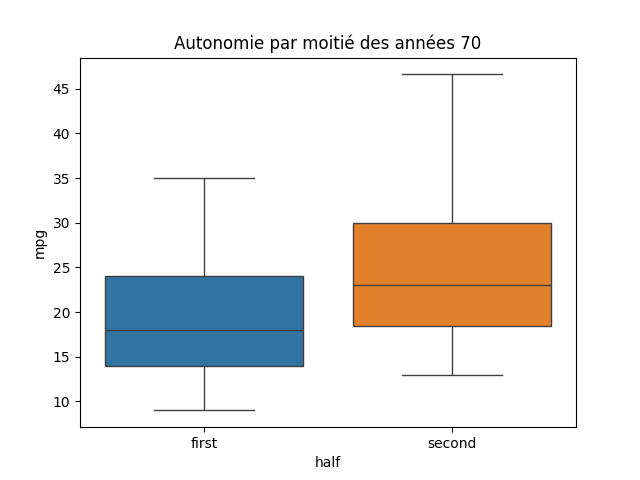
Nombre de points
df_temp.groupby('half').size()
half first 152 second 186 dtype: int64
Variance
df_temp.groupby('half')['mpg'].var()
half first 35.761197 second 58.022495 Name: mpg, dtype: float64
Conditions pour appliquer un test de Student (TTest ind)
1°) Données normales ou plus de 30 points : OK avec 152/186 points
2°) Observations indépendantes : Oui, les modèles de voitures sont indépendants les unsdes autres
3°) Variances similaires entre les 2 groupes : A priori non => Comparatif Test de Student et Test de Welsh
1°) Données normales ou plus de 30 points : OK avec 152/186 points
2°) Observations indépendantes : Oui, les modèles de voitures sont indépendants les unsdes autres
3°) Variances similaires entre les 2 groupes : A priori non => Comparatif Test de Student et Test de Welsh
Test de Student (2 échantillons indépendants) - Hypothèse 0
H0: mpg moyen groupe A = mpg moyen groupe B
Groupe A = Tous les modèles 70-74 ('first')
Groupe B = Tous les modèles 75-80 ('second')
H0: mpg moyen groupe A = mpg moyen groupe B
Groupe A = Tous les modèles 70-74 ('first')
Groupe B = Tous les modèles 75-80 ('second')
Test de Student
first_half = df_temp.query("`half` == 'first'")
second_half = df_temp.query("`half` == 'second'")
ttest_ind(first_half['mpg'], second_half['mpg'], equal_var=True)
TtestResult(statistic=np.float64(-6.974712842718591), pvalue=np.float64(1.6352499382971174e-11), df=np.float64(336.0))
→
Test de Student : La p-value est inférieure à alpha (0.02): On rejette donc H0 !
Test de Welsh
first_half = df_temp.query("`half` == 'first'")
second_half = df_temp.query("`half` == 'second'")
ttest_ind(first_half['mpg'], second_half['mpg'], equal_var=False)
TtestResult(statistic=np.float64(-7.1437825589430295), pvalue=np.float64(5.683745347453685e-12), df=np.float64(335.486240224964))
→
Test de Welsh : La p-value est inférieure à alpha (0.02): On rejette donc H0 !
3. Un constructeur automobile américain affirme que les voitures américaines à 4 cylindres ont en moyenne la même accélération que les voitures américaines à 6 cylindres. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02).
Moyennes
df.query("`origin` == 'usa' & `model_year` <= 80 ").groupby('cylinders')['acceleration'].mean()
cylinders 4 16.531915 6 16.550746 8 12.896078 Name: acceleration, dtype: float64
Variances
df.query("`origin` == 'usa' & `model_year` <= 80 ").groupby('cylinders')['acceleration'].var()
cylinders 4 4.760481 6 3.681325 8 4.633252 Name: acceleration, dtype: float64
Nombre de points
df.query("`origin` == 'usa' & `model_year` <= 80 ").groupby('cylinders')['acceleration'].size()
cylinders 4 47 6 67 8 102 Name: acceleration, dtype: int64
Conditions pour appliquer un test de Student (TTest ind)
1°) Données normales ou plus de 30 points : OK avec 47/67 points
2°) Observations indépendantes : Oui, les modèles de voitures sont indépendants les unsdes autres
3°) Variances similaires entre les 2 groupes : Oui
1°) Données normales ou plus de 30 points : OK avec 47/67 points
2°) Observations indépendantes : Oui, les modèles de voitures sont indépendants les unsdes autres
3°) Variances similaires entre les 2 groupes : Oui
Test de Student (2 échantillons indépendants) - Hypothèse 0
H0: Les voitures américaine 4 cylindres ont en moyenne la même accélaration que les voitures américaines 6 cylindres
H0: Les voitures américaine 4 cylindres ont en moyenne la même accélaration que les voitures américaines 6 cylindres
Test de Student
four_cylinders = df.query("`origin` == 'usa' & `model_year` <= 80 & `cylinders` == 4")
six_cylinders = df.query("`origin` == 'usa' & `model_year` <= 80 & `cylinders` == 6")
ttest_ind(four_cylinders['acceleration'], six_cylinders['acceleration'], equal_var=False)
TtestResult(statistic=np.float64(-0.04764277622265472), pvalue=np.float64(0.9621055550215347), df=np.float64(90.81728092025011))
→
Test de Student : La p-value est supérieure à alpha (0.02): On ne peut donc pas rejetter H0
4. Un collectionneur de voitures affirme que parmi les voitures Ford des années 1970-1982, il y a 25% de 4 cylindres, 25% de 6 cylindres et 50% de 8 cylindres. Testez son affirmation et concluez avec un niveau de confiance de 98%.
Test d'hypothèse nulle
H0:
parmi les voitures Ford des années 1970-1982, il y a :
- 25 % de 4 cylindres
- 25 % de 6 cylindres
- 50 % de 8 cylindres
H0:
parmi les voitures Ford des années 1970-1982, il y a :
- 25 % de 4 cylindres
- 25 % de 6 cylindres
- 50 % de 8 cylindres
df.head()
mpg cylinders displacement ... model_year origin name 0 18.0 8 307.0 ... 70 usa chevrolet chevelle malibu 1 15.0 8 350.0 ... 70 usa buick skylark 320 2 18.0 8 318.0 ... 70 usa plymouth satellite 3 16.0 8 304.0 ... 70 usa amc rebel sst 4 17.0 8 302.0 ... 70 usa ford torino [5 rows x 9 columns]
df['name']
0 chevrolet chevelle malibu
1 buick skylark 320
2 plymouth satellite
3 amc rebel sst
4 ford torino
...
393 ford mustang gl
394 vw pickup
395 dodge rampage
396 ford ranger
397 chevy s-10
Name: name, Length: 398, dtype: object
df['name'].str.contains('ford')
0 False
1 False
2 False
3 False
4 True
...
393 True
394 False
395 False
396 True
397 False
Name: name, Length: 398, dtype: bool
df_ford = df[df['name'].str.contains('ford')]
mpg cylinders displacement ... model_year origin name 4 17.0 8 302.0 ... 70 usa ford torino 5 15.0 8 429.0 ... 70 usa ford galaxie 500 17 21.0 6 200.0 ... 70 usa ford maverick 25 10.0 8 360.0 ... 70 usa ford f250 32 25.0 4 98.0 ... 71 usa ford pinto 36 19.0 6 250.0 ... 71 usa ford torino 500 40 14.0 8 351.0 ... 71 usa ford galaxie 500 43 13.0 8 400.0 ... 71 usa ford country squire (sw) 48 18.0 6 250.0 ... 71 usa ford mustang 61 21.0 4 122.0 ... 72 usa ford pinto runabout 65 14.0 8 351.0 ... 72 usa ford galaxie 500 74 13.0 8 302.0 ... 72 usa ford gran torino (sw) 80 22.0 4 122.0 ... 72 usa ford pinto (sw) 88 14.0 8 302.0 ... 73 usa ford gran torino 92 13.0 8 351.0 ... 73 usa ford ltd 100 18.0 6 250.0 ... 73 usa ford maverick 104 12.0 8 400.0 ... 73 usa ford country 112 19.0 4 122.0 ... 73 usa ford pinto 126 21.0 6 200.0 ... 74 usa ford maverick 130 26.0 4 122.0 ... 74 usa ford pinto 136 16.0 8 302.0 ... 74 usa ford gran torino 139 14.0 8 302.0 ... 74 usa ford gran torino (sw) 155 15.0 6 250.0 ... 75 usa ford maverick 159 14.0 8 351.0 ... 75 usa ford ltd 166 13.0 8 302.0 ... 75 usa ford mustang ii 168 23.0 4 140.0 ... 75 usa ford pinto 174 18.0 6 171.0 ... 75 usa ford pinto 190 14.5 8 351.0 ... 76 usa ford gran torino 193 24.0 6 200.0 ... 76 usa ford maverick 200 18.0 6 250.0 ... 76 usa ford granada ghia 206 26.5 4 140.0 ... 76 usa ford pinto 214 13.0 8 302.0 ... 76 usa ford f108 228 18.5 6 250.0 ... 77 usa ford granada 232 16.0 8 351.0 ... 77 usa ford thunderbird 236 25.5 4 140.0 ... 77 usa ford mustang ii 2+2 245 36.1 4 98.0 ... 78 usa ford fiesta 254 20.2 6 200.0 ... 78 usa ford fairmont (auto) 255 25.1 4 140.0 ... 78 usa ford fairmont (man) 264 18.1 8 302.0 ... 78 usa ford futura 282 22.3 4 140.0 ... 79 usa ford fairmont 4 286 17.6 8 302.0 ... 79 usa ford ltd landau 290 15.5 8 351.0 ... 79 usa ford country squire (sw) 314 26.4 4 140.0 ... 80 usa ford fairmont 336 23.6 4 140.0 ... 80 usa ford mustang cobra 351 34.4 4 98.0 ... 81 usa ford escort 4w 352 29.9 4 98.0 ... 81 usa ford escort 2h 365 20.2 6 200.0 ... 81 usa ford granada gl 373 24.0 4 140.0 ... 82 usa ford fairmont futura 389 22.0 6 232.0 ... 82 usa ford granada l 393 27.0 4 140.0 ... 82 usa ford mustang gl 396 28.0 4 120.0 ... 82 usa ford ranger [51 rows x 9 columns]
Cylinders
df_ford['cylinders'].value_counts(normalize=True)
cylinders 8 0.392157 4 0.352941 6 0.254902 Name: proportion, dtype: float64
Observed frequencies
observed_frequencies = df_ford['cylinders'].value_counts().sort_index()
cylinders 4 18 6 13 8 20 Name: count, dtype: int64
Expected frequencies
expected_frequencies = np.array([0.25, 0.25, 0.5]) * observed_frequencies.sum()
[12.75 12.75 25.5 ]
ChiSquare
result = chisquare(f_exp=expected_frequencies, f_obs=observed_frequencies)
Power_divergenceResult(statistic=np.float64(3.352941176470588), pvalue=np.float64(0.18703292871671046))
→
Est-ce que la p-value est inférieure à 0.02 : Non
Nous n'avons pas de preuves suffisament importantes pour rejeter H0 au seuil alpha=0.02
Juste qu'à preuve du contraire, on peut croire l'affirmation du collectionneur
Nous n'avons pas de preuves suffisament importantes pour rejeter H0 au seuil alpha=0.02
Juste qu'à preuve du contraire, on peut croire l'affirmation du collectionneur
5. Les voitures à 4 cylindres ont en moyenne la même consommation d'essence au Japon, en Europe et aux États-Unis, dans les années 1970-1982. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02).
Moyennes
df.query("`cylinders` == 4").groupby('origin')['mpg'].mean())
origin europe 28.411111 japan 31.595652 usa 27.840278 Name: mpg, dtype: float64
Variances
df.query("`cylinders` == 4").groupby('origin')['mpg'].var())
origin europe 41.505842 japan 29.547775 usa 20.698496 Name: mpg, dtype: float64
Anova
ma_liste = df.query("`cylinders` == 4").groupby('origin')['mpg'].apply(list)
f_oneway(*ma_liste)
F_onewayResult(statistic=np.float64(9.411845545485601), pvalue=np.float64(0.00012379894210177303))
→
Est-ce que la p-value est inférieure à 0.02 : Oui
Nous devons rejeter l'hypothèse H0 au seuil alpha=0.02
Nous devons rejeter l'hypothèse H0 au seuil alpha=0.02
6. Les voitures européennes et japonaises ont en moyenne le même nombre de chevaux. Testez cette affirmation et concluez avec un niveau de confiance de 98 % (alpha = 0,02).
Analyse des données
df.groupby('origin')['horsepower'].describe()
count mean std min 25% 50% 75% max origin europe 68.0 80.558824 20.157871 46.0 69.75 76.5 90.0 133.0 japan 79.0 79.835443 17.819199 52.0 67.00 75.0 95.0 132.0 usa 245.0 119.048980 39.897790 52.0 88.00 105.0 150.0 230.0
Test d'hypothèse nulle
Test de Student avec H0: Les voitures du Japon et de l'Europe ont en moyenne le même nombre de chevaux
Test de Student avec H0: Les voitures du Japon et de l'Europe ont en moyenne le même nombre de chevaux
Conditions pour appliquer un test de Student (TTest ind)
1°) Données normales ou plus de 30 points : OK avec 68/79 points
2°) Observations indépendantes : Oui, les modèles de voitures sont indépendants les unsdes autres
3°) Variances similaires entre les 2 groupes : Oui (20 et 18)
1°) Données normales ou plus de 30 points : OK avec 68/79 points
2°) Observations indépendantes : Oui, les modèles de voitures sont indépendants les unsdes autres
3°) Variances similaires entre les 2 groupes : Oui (20 et 18)
Test de Student
japan = df.query("`origin` == 'japan'")
europe = df.query("`origin` == 'europe'")
ttest_ind(japan['horsepower'], europe['horsepower'])
TtestResult(statistic=np.float64(nan), pvalue=np.float64(nan), df=np.float64(nan))
→
Est-ce que la p-value est inférieure à 0.02 : Non (0.82)
Nous ne pouvons pas rejeter l'hypothèse H0 au seuil alpha=0.02
Nous ne pouvons pas rejeter l'hypothèse H0 au seuil alpha=0.02
→
Est-ce que la p-value est inférieure à 0.02 : Non (0.49)
Nous ne pouvons pas rejeter l'hypothèse H0 au seuil alpha=0.02
Nous ne pouvons pas rejeter l'hypothèse H0 au seuil alpha=0.02
7. Un spécialiste vous dit que les constructeurs Ford et Dodge produisaient dans les années 70-82 des voitures avec un nombre de cylindres équivalent. Testez cette affirmation et concluez avec un niveau de confiance de 98% (alpha = 0,02)
filtered_df = df[df['name'].str.contains('ford|dodge', case=False, na=False)]
mpg cylinders displacement ... model_year origin name 4 17.0 8 302.0 ... 70 usa ford torino 5 15.0 8 429.0 ... 70 usa ford galaxie 500 10 15.0 8 383.0 ... 70 usa dodge challenger se 17 21.0 6 200.0 ... 70 usa ford maverick 25 10.0 8 360.0 ... 70 usa ford f250 .. ... ... ... ... ... ... ... 389 22.0 6 232.0 ... 82 usa ford granada l 391 36.0 4 135.0 ... 82 usa dodge charger 2.2 393 27.0 4 140.0 ... 82 usa ford mustang gl 395 32.0 4 135.0 ... 82 usa dodge rampage 396 28.0 4 120.0 ... 82 usa ford ranger [79 rows x 9 columns]
Nouvelle colonne 'Brand'
filtered_df['brand'] = filtered_df['name'].apply(lambda x: 'ford' if 'ford' in x else 'dodge')
mpg cylinders displacement ... origin name brand 4 17.0 8 302.0 ... usa ford torino ford 5 15.0 8 429.0 ... usa ford galaxie 500 ford 10 15.0 8 383.0 ... usa dodge challenger se dodge 17 21.0 6 200.0 ... usa ford maverick ford 25 10.0 8 360.0 ... usa ford f250 ford .. ... ... ... ... ... ... ... 389 22.0 6 232.0 ... usa ford granada l ford 391 36.0 4 135.0 ... usa dodge charger 2.2 dodge 393 27.0 4 140.0 ... usa ford mustang gl ford 395 32.0 4 135.0 ... usa dodge rampage dodge 396 28.0 4 120.0 ... usa ford ranger ford [79 rows x 10 columns]
Tableau de contingence
pd.crosstab(filtered_df['brand'], filtered_df['cylinders'])
cylinders 4 6 8 brand dodge 12 4 12 ford 18 13 20
Chi Square Contingency
chi2_contingency(pd.crosstab(filtered_df['brand'], filtered_df['cylinders']))
Chi2ContingencyResult(statistic=np.float64(1.3859820398747735), pvalue=np.float64(0.5000780864081316), dof=2, expected_freq=array([[10.63291139, 6.02531646, 11.34177215],
[19.36708861, 10.97468354, 20.65822785]]))